【题目】在四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随着点
的位置随着点![]() 的位置变化而变化.
的位置变化而变化.

(1)如图1,当点![]() 在四边形
在四边形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是________,
的数量关系是________,![]() 与
与![]() 的位置关系是_______;
的位置关系是_______;
(2)如图2,当点![]() 在四边形
在四边形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;
外部时,(1)中的结论是否还成立?若成立,请予以证明;
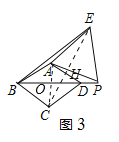
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,则线段
,则线段![]() ______,
______,![]() ________.
________.
参考答案:
【答案】(1)PB=EC,CE⊥AD;(2)结论仍然成立,理由见解析;(3)DP= 10,EP=![]()
【解析】
(1)如图1中,结论:PB=EC,CE⊥AD.连接AC,延长CE交AD于H,根据“SAS”证明△BAP≌△CAE即可解决问题;
(2)结论仍然成立.连接AC交BD于O,设CE交AD于H.证明方法与(1)类似;
(3)首先证明△BAP≌△CAE,解直角三角形求出AP,DP,OA即可解决问题;
解:(1)如图1中,结论:PB=EC,CE⊥AD.
理由:连接AC,延长CE交AD于H.
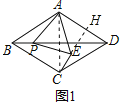
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∵∠BAC=∠PAE,
∴∠BAP=∠CAE,
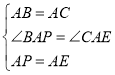 ,
,
∴△BAP≌△CAE,
∴BP=CE,∠ABP=∠ACE=30°,
∵∠CAH=60°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,即CE⊥AD.
故答案为PB=EC,CE⊥AD;
(2)结论仍然成立.
理由:选图2,连接AC交BD于O,设CE交AD于H.
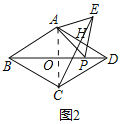
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∴∠BAP=∠CAE.
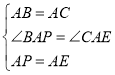 ,
,
∴△BAP≌△CAE,
∴BP=CE,∠PBA=∠ACE=30°,
∵∠CAH=60°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,即CE⊥AD.
(3)选图3,连接AC交BD于O,连接CE交AD于H.
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∴∠BAP=∠CAE.
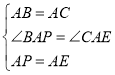 ,
,
∴△BAP≌△CAE,
∴BP=CE,∠ABP=∠ACE=30°,
∵∠CAH=60°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,即CE⊥AD.
在菱形ABCD中,AD∥BC,
∴EC⊥BC,
∵BC=AB=2![]() ,BE=
,BE=![]() ,
,
在Rt△BCE中,EC=![]() =7,
=7,
∴BP=CE=7,
∵AC与BD是菱形的对角线,
∴∠ABD=![]() ∠ABC=30°,AC⊥BD,
∠ABC=30°,AC⊥BD,
∴OA=![]() AB=
AB=![]() ,
,
∴BO=OD=![]() =3,
=3,
∴BD=2BO=6,
∴DP=BP-BD=7-6=1,
∴OP=OD+DP=4,
在Rt△AOP中,AP=![]() ,
,
∴EP=AP=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
【答案】y=﹣5x2+2x﹣1
【解析】试题分析:根据二次函数的定义得到m2+m﹣4=2且m﹣2≠0,由此求得m的值,进而得到该二次函数的解析式.
试题解析:依题意得:m2+m﹣4=2且m﹣2≠0. 即(m﹣2)(m+3)=0且m﹣2≠0,
解得m=﹣3,
则该二次函数的解析式为y=﹣5x2+2x﹣1
【题型】解答题
【结束】
21【题目】如图,在ABCD中,EF∥AB,FG∥ED,DE:DA=2:5,EF=4,求线段CG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,M,N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞,工程人员为计算工程量,必须测量M、N两点之间的直线距离.选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米,AN=1.8千米,AB=54米,BC=45米,AC=30米,求M、N两点之间的直线距离.

【答案】M、N两点之间的直线距离为1500米.
【解析】试题分析:先根据相似三角形的判定得出△ABC∽△AMN,再利用相似三角形的性质解答即可.
试题解析:在△ABC与△AMN中,
 ,
,  =
=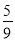 ,∴
,∴ ,又∵∠A=∠A,
,又∵∠A=∠A,∴△ABC∽△AMN,∴
 ,即
,即 ,
,解得:MN=1500米,
答:M、N两点之间的直线距离是1500米;
考点:相似三角形的应用.
【题型】解答题
【结束】
23【题目】如图,在△ADC中,点B是边DC上的一点,∠DAB=∠C,
 .若△ADC的面积为18cm,求△ABC的面积.
.若△ADC的面积为18cm,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是函数
是函数 上两点,
上两点, 为一动点,作
为一动点,作 轴,
轴, 轴,下列说法正确的是( )
轴,下列说法正确的是( )
①
 ;②
;② ;③若
;③若 ,则
,则 平分
平分 ;④若
;④若 ,则
,则
A. ①③ B. ②③ C. ②④ D. ③④
-
科目: 来源: 题型:
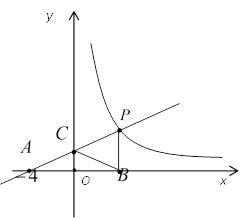
查看答案和解析>>【题目】如图,直线
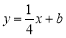 与反比例函数
与反比例函数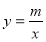 的图象交于点
的图象交于点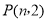 ,与
,与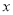 轴交于点
轴交于点 ,与
,与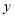 轴交于点
轴交于点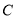 ,
,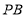 垂直
垂直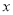 轴于点
轴于点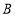 ,且
,且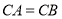 .
.
(1)仔细观察图形,直接写出
 ;
;(2)求
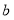 和
和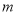 的值;
的值;(3)在反比例函数图象上是否存在点
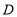 ,使四边形
,使四边形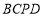 为平行四边形,如果存在,求出点
为平行四边形,如果存在,求出点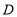 的坐标,如果不存在,请说明理由.
的坐标,如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于点O, ∠AOM=90°,

(1)如图1,若OC平分∠AOM.求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数;
相关试题

