【题目】如图,直线AB与CD相交于点O, ∠AOM=90°,

(1)如图1,若OC平分∠AOM.求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数;
参考答案:
【答案】(1)∠AOD=135°;(2)∠MON=54°.
【解析】试题分析:(1)根据角平分线的定义求出∠AOC=45°,然后根据邻补角的定义求解即可;
(2)设∠NOB=x°,∠BOC=4x°,根据角平分线的定义表示出∠COM=∠MON=![]() ∠CON,再根据∠BOM列出方程求解x,然后求解即可.
∠CON,再根据∠BOM列出方程求解x,然后求解即可.
(1)∵∠AOM=90°,OC平分∠AOM,∴∠AOC=![]() ∠AOM=
∠AOM=![]() x90°=45°,
x90°=45°,
∵∠AOC+∠AOD=180°,∴∠AOD=180°-∠AOC=180°-45°=135°;
(2)∵∠BOC=4∠NOB,设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB-∠BON=4x°-x°=3x°,∵OM平分∠CON,
∴∠COM=∠MON=![]() ∠CON=
∠CON=![]() x°,∵∠BOM=
x°,∵∠BOM=![]() x+x=90,∴x=36,
x+x=90,∴x=36,
∴∠MON=![]() x°=54°,即∠MON的度数为54°.
x°=54°,即∠MON的度数为54°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形
 中,
中, ,
, ,点
,点 是射线
是射线 上一动点,以
上一动点,以 为边向右侧作等边
为边向右侧作等边 ,点
,点 的位置随着点
的位置随着点 的位置变化而变化.
的位置变化而变化.
(1)如图1,当点
 在四边形
在四边形 内部或边上时,连接
内部或边上时,连接 ,
,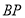 与
与 的数量关系是________,
的数量关系是________, 与
与 的位置关系是_______;
的位置关系是_______;(2)如图2,当点
 在四边形
在四边形 外部时,(1)中的结论是否还成立?若成立,请予以证明;
外部时,(1)中的结论是否还成立?若成立,请予以证明;(3)如图3,当点
 在线段
在线段 的延长线上时,连接
的延长线上时,连接 ,若
,若 ,
,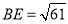 ,则线段
,则线段 ______,
______, ________.
________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是函数
是函数 上两点,
上两点, 为一动点,作
为一动点,作 轴,
轴, 轴,下列说法正确的是( )
轴,下列说法正确的是( )
①
 ;②
;② ;③若
;③若 ,则
,则 平分
平分 ;④若
;④若 ,则
,则
A. ①③ B. ②③ C. ②④ D. ③④
-
科目: 来源: 题型:
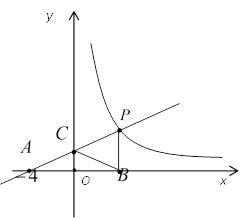
查看答案和解析>>【题目】如图,直线
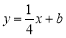 与反比例函数
与反比例函数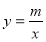 的图象交于点
的图象交于点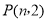 ,与
,与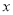 轴交于点
轴交于点 ,与
,与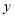 轴交于点
轴交于点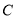 ,
,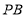 垂直
垂直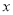 轴于点
轴于点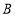 ,且
,且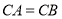 .
.
(1)仔细观察图形,直接写出
 ;
;(2)求
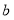 和
和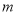 的值;
的值;(3)在反比例函数图象上是否存在点
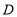 ,使四边形
,使四边形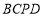 为平行四边形,如果存在,求出点
为平行四边形,如果存在,求出点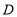 的坐标,如果不存在,请说明理由.
的坐标,如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中, 点
点 是矩形
是矩形 内一动点,且
内一动点,且 ,则
,则 的最小值为_____.
的最小值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ADC中,点B是边DC上的一点,∠DAB=∠C,
 .若△ADC的面积为18cm,求△ABC的面积.
.若△ADC的面积为18cm,求△ABC的面积.
【答案】10
【解析】试题分析:根据相似三角形的判定定理得到△ADC∽△BAD,根据相似三角形的面积比等于相似比的平方即可得到结论.
试题解析:∵∠DAB=∠C,∠D=∠D, ∴△ADC∽△BAD,
∴
 ,
,∵△ADC的面积为18cm2 ,
∴△BDA的面积为8cm2 ,
∴△ABC的面积=△ADC的面积﹣△BDA的面积=10cm2
【题型】解答题
【结束】
24【题目】如图,在网格图中的△ABC与△DEF是否成位似图形?说明理由.如果是,同时指出它们的位似中心.

相关试题

