【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )

A. 504m2 B. ![]() m2 C.
m2 C. ![]() m2 D. 1009m2
m2 D. 1009m2
参考答案:
【答案】A
【解析】
由OA4n=2n知OA2017=![]() +1=1009,据此得出A2A2018=1009-1=1008,据此利用三角形的面积公式计算可得.
+1=1009,据此得出A2A2018=1009-1=1008,据此利用三角形的面积公式计算可得.
由题意知OA4n=2n,
∴OA2016=2016÷2=1008,即A2016坐标为(1008,0),
∴A2018坐标为(1009,1),
则A2A2018=1009-1=1008(m),
∴![]() =
=![]() A2A2018×A1A2=
A2A2018×A1A2=![]() ×1008×1=504(m2).
×1008×1=504(m2).
故选:A.
-
科目: 来源: 题型:
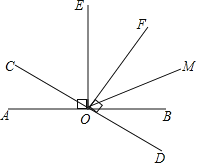
查看答案和解析>>【题目】如图,已知直线AB与CD相交于点0,OE⊥AB,OF⊥CD,OM是∠BOF的角平分线
(1)若∠AOC=25°,求∠BOD和∠COE的度数.
(2)若∠AOC=a,求∠EOM的度数(用含a的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时
 张用A方法,其余用B方法。
张用A方法,其余用B方法。(1)用
 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,面积为30的长方形OABC的边OA在数轴上,O为原点,OC=5.将长方形OABC沿数轴水平移动,O,A,B,C移动后的对应点分别记为O1, A1, B1, C1,移动后的长方形O1A1B1C1与原长方形OABC重叠部分的面积记为S
(1)当S恰好等于原长方形面积的一半时,数轴上点A1表示的数是多少?
(2)设点A的移动距离AA1=x
①当S=10时,求x的值;
②D为线段AA1的中点,点E在线段OO1上,且OE=
 OO1,当点D,E所表示的数互为相反数时,求x的值.
OO1,当点D,E所表示的数互为相反数时,求x的值.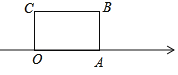
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了招聘一名优秀教师,对入选的三名候选人进行教学技能与专业知识两种考核,现将甲、乙、丙三人的考核成绩统计如下:

(1)如果校方认为教师的教学技能水平与专业知识水平同等重要,那么候选人 将被录取.
(2)如果校方认为教师的教学技能水平比专业知识水平重要,并分别赋予它们6和4的权.计算他们赋权后各自的平均成绩,并说明谁将被录取.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,长方形ABCD沿着直线DE和EF折叠,使得AB的对应点
 和点E在同一条直线上。
和点E在同一条直线上。(1)求∠DEF的度数;
(2)如图2,若再次沿着直线EM和EN折叠使得A、B的对应点
 分别落在DE和EF上,∠AEM=34°,求∠BEN的度数。
分别落在DE和EF上,∠AEM=34°,求∠BEN的度数。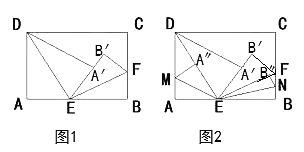
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,点
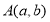 满足
满足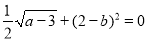 ,
,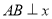 轴于点
轴于点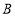 .
.
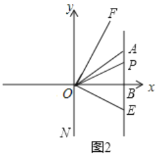
(1)点
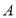 的坐标为 ,点
的坐标为 ,点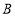 的坐标为 ;
的坐标为 ;(2)如图1,若点
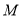 在
在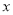 轴上,连接
轴上,连接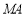 ,使
,使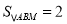 ,求出点
,求出点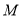 的坐标;
的坐标;(3)如图2,
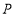 是线段
是线段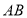 所在直线上一动点,连接
所在直线上一动点,连接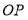 ,
,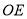 平分
平分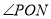 ,交直线
,交直线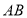 于点
于点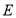 ,作
,作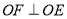 ,当点
,当点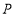 在直线
在直线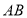 上运动过程中,请探究
上运动过程中,请探究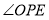 与
与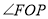 的数量关系,并证明.
的数量关系,并证明.
相关试题

