【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.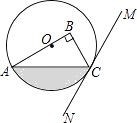
(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.
参考答案:
【答案】
(1)解:MN是⊙O切线.
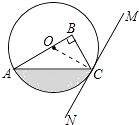
理由:连接OC.
∵OA=OC,
∴∠OAC=∠OCA,
∵∠BOC=∠A+∠OCA=2∠A,∠BCM=2∠A,
∴∠BCM=∠BOC,
∵∠B=90°,
∴∠BOC+∠BCO=90°,
∴∠BCM+∠BCO=90°,
∴OC⊥MN,
∴MN是⊙O切线.
(2)解:由(1)可知∠BOC=∠BCM=60°,
∴∠AOC=120°,
在Rt△BCO中,OC=OA=4,∠BCO=30°,
∴BO= ![]() OC=2,BC=2
OC=2,BC=2 ![]()
∴S阴=S扇形OAC﹣S△OAC= ![]() ﹣
﹣ ![]() =
= ![]() ﹣4
﹣4 ![]() .
.
【解析】(1)要证直线MN与⊙O的切线,连接OC.易证∠BOC=2∠A,由∠BCM=2∠A,得出∠BOC=∠BCM,在Rt△OBC中,根据直角三角形两锐角互余,可推出OC⊥MN,即可得出结论。
(2)先求出∠AOC的度数,在Rt△BCO中,利用解直角三角形求出BO、BC的长,根据S阴=S扇形OAC﹣S△OAC,即可求出阴影部分的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数y=﹣
 在第二象限内图象上一点,点B是反比例函数y=
在第二象限内图象上一点,点B是反比例函数y=  在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,求△AOB的面积.
在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1+∠2=180°,∠3=∠B,试说明DE∥BC.下面是部分推导过程,请你在括号内填上推导依据或内容:
证明:∵∠1+∠2=180°(已知)
∠1=∠4 ( )
∴∠2+∠4=180°(等量代换)
∵EH∥AB( )
∴∠B= ( )
∵∠3=∠B(已知)
∴∠3=∠EHC(等量代换)
∴DE∥BC ( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将三角形ABC向左平移至点B与原点重合,得三角形A′OC′.
(1)直接写出三角形ABC的三个顶点的坐标A B C ;
(2)画出三角形A′OC′;
(3)求三角形ABC的面积;
(4)直接与出A′C′与y轴交点的坐标 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在抗洪抢险中,解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民,早晨从
 地出发,晚上到达
地出发,晚上到达 地,约定向东为正方向,当天的航行路程记录如下(单位:千米):
地,约定向东为正方向,当天的航行路程记录如下(单位:千米): ,
, ,
, ,
,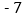 ,
, ,
,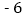 ,
, ,
, .
.(1)请你帮忙确定
 地位于
地位于 地的什么方向,距离
地的什么方向,距离 地多少千米?
地多少千米? (2)若冲锋舟每千米耗油
 升,邮箱容量为
升,邮箱容量为 升,求冲锋舟当天救灾过程中至少还需补充多少升油?
升,求冲锋舟当天救灾过程中至少还需补充多少升油? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点
 ,第二次点
,第二次点 跳动至点
跳动至点 第三次点
第三次点 跳动至点
跳动至点 ,第四次点
,第四次点 跳动至点
跳动至点 ……,依此规律跳动下去,则点
……,依此规律跳动下去,则点 与点
与点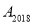 之间的距离是( )
之间的距离是( )
A. 2017B. 2018C. 2019D. 2020
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,第一次将
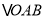 变换成
变换成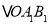 ,第二次将
,第二次将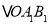 变换成
变换成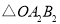 ,第三次将
,第三次将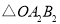 变换成
变换成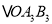 ,已知:
,已知: 、
、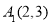 、
、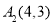 、
、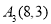 、
、 、
、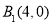
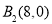 、
、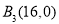 .若将
.若将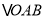 进行了
进行了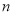 (
(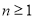 ,且
,且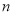 为整数)次变换,得到
为整数)次变换,得到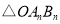 ,推测
,推测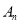 的坐标是_____,
的坐标是_____,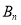 点的坐标是_______.
点的坐标是_______.
相关试题

