【题目】如果一个圆上所有的点都在一个角的内部或边上,那么称这个圆为该角的角内圆.特别地,当这个圆与角的至少一边相切时,称这个圆为该角的角内相切圆.在平面直角坐标系xOy中,点E,F分别在x轴的正半轴和y轴的正半轴上.
(1)分别以点A(1,0),B(1,1),C(3,2)为圆心,1为半径作圆,得到⊙A,⊙B和⊙C,其中是∠EOF的角内圆的是 ;
(2)如果以点D(t,2)为圆心,以1为半径的⊙D为∠EOF的角内圆,且与直线y=x有公共点,求t的取值范围;
(3)点M在第一象限内,如果存在一个半径为1且过点P(2,2![]() )的圆为∠EMO的角内相切圆,直接写出∠EOM的取值范围.
)的圆为∠EMO的角内相切圆,直接写出∠EOM的取值范围.
参考答案:
【答案】(1)⊙B,⊙C;(2)1≤t≤2+![]() ;(3)60°≤∠EOM<90°
;(3)60°≤∠EOM<90°
【解析】
(1)画出图象,根据角内相切圆的定义判断即可.
(2)求出两种特殊位置时t的值即可判断.
(3)如图3中,连接OP,OM.首先求出∠POE,根据图象可知当射线OM在∠POF的内部(包括射线OP,不包括射线OF)时,存在一个半径为1且过点P(2,2![]() )的圆为∠EMO的角内相切圆.
)的圆为∠EMO的角内相切圆.
(1)如图1中,观察图象可知,⊙B和⊙C,其中是∠EOF的角内圆.
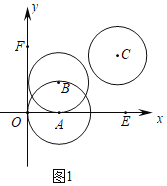
故答案为:⊙B,⊙C.
(2)解:如图,
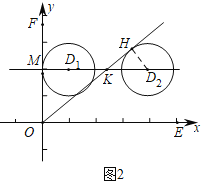
当⊙D1与y轴相切时,设切点为M,则MD1=1,可得t1=1.
当⊙D2与y=x相切时,设切点为H,连接HD2,设直线y=x与直线y=2交于点K,则△HKD2,△MOK都是等腰直角三角形,
∵KH=HD2=1,
∴KD2=![]() ,
,
∵OM=MK=2,
∴MD2=MK+KD2=2+![]()
可得t2=2+![]() ,
,
观察图象可知,满足条件的t的取值范围是1≤t≤2+![]() .
.
(3)如图3中,连接OP,OM.
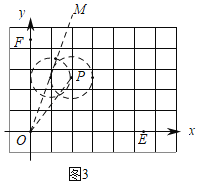
∵P(2,2![]() ),
),
∴tan∠POE=![]() =
=![]() ,
,
∴∠POE=60°,
观察图象可知当射线OM在∠POF的内部(包括射线OP,不包括射线OF)时,存在一个半径为1且过点P(2,2![]() )的圆为∠EMO的角内相切圆,
)的圆为∠EMO的角内相切圆,
∴60°≤∠EOM<90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是以点O为圆心,AB为直径的半圆上的动点(不与点A,B重合),AB=6cm,过点C作CD⊥AB于点D,E是CD的中点,连接AE并延长交
 于点F,连接FD.小腾根据学习函数的经验,对线段AC,CD,FD的长度之间的关系进行了探究.
于点F,连接FD.小腾根据学习函数的经验,对线段AC,CD,FD的长度之间的关系进行了探究.
下面是小腾的探究过程,请补充完整:
(1)对于点C在
 上的不同位置,画图、测量,得到了线段AC,CD,FD的长度的几组值,如表:
上的不同位置,画图、测量,得到了线段AC,CD,FD的长度的几组值,如表:位置1
位置2
位置3
位置4
位置5
位置6
位置7
位置8
AC/cm
0.1
0.5
1.0
1.9
2.6
3.2
4.2
4.9
CD/cm
0.1
0.5
1.0
1.8
2.2
2.5
2.3
1.0
FD/cm
0.2
1.0
1.8
2.8
3.0
2.7
1.8
0.5
在AC,CD,FD的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;

(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解答问题:当CD>DF时,AC的长度的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2﹣2ax.
(1)二次函数图象的对称轴是直线x= ;
(2)当0≤x≤3时,y的最大值与最小值的差为4,求该二次函数的表达式;
(3)若a<0,对于二次函数图象上的两点P(x1,y1),Q(x2,y2),当t≤x1≤t+1,x2≥3时,均满足y1≥y2,请结合函数图象,直接写出t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=120°,点P为射线OA上一动点(不与点O重合),点C为∠AOB内部一点,连接CP,将线段CP绕点C顺时针旋转60°得到线段CQ,且点Q恰好落在射线OB上,不与点O重合.
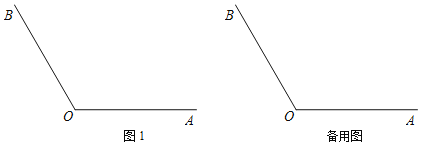
(1)依据题意补全图1;
(2)用等式表示∠CPO与∠CQO的数量关系,并证明;
(3)连接OC,写出一个OC的值,使得对于任意点P,总有OP+OQ=4,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=kx2+(2k+1)x+1(k为实数).
(1)对于任意实数k,函数图象一定经过点(﹣2,﹣1)和点_____;
(2)对于任意正实数k,当x>m时,y随着x的增大而增大,写出一个满足题意的m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 ,点
,点 在直线
在直线 上,以点
上,以点 为圆心,适当长度为半径画弧,分别交直线
为圆心,适当长度为半径画弧,分别交直线 ,
,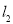 于
于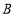 ,
,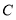 两点,以点
两点,以点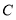 为圆心,
为圆心, 长为半径画弧,与前弧交于点
长为半径画弧,与前弧交于点 (不与点
(不与点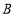 重合),连接
重合),连接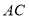 ,
,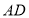 ,
, ,
,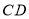 ,其中
,其中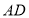 交
交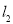 于点
于点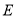 .若
.若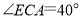 ,则下列结论错误的是( )
,则下列结论错误的是( )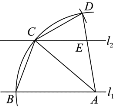
A.
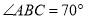 B.
B.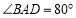 C.
C.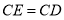 D.
D.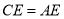
-
科目: 来源: 题型:
查看答案和解析>>【题目】生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的
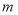 天数据,整理后绘制成统计表进行分析.
天数据,整理后绘制成统计表进行分析.日均可回收物回收量(千吨)
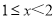
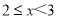

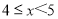
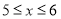
合计
频数
1
2
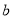
3
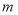
频率
0.05
0.10
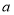
0.15
1
表中
 组的频率
组的频率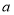 满足
满足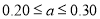 .
.下面有四个推断:
①表中
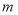 的值为20;
的值为20;②表中
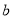 的值可以为7;
的值可以为7;③这
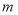 天的日均可回收物回收量的中位数在
天的日均可回收物回收量的中位数在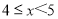 组;
组;④这
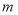 天的日均可回收物回收量的平均数不低于3.
天的日均可回收物回收量的平均数不低于3.所有合理推断的序号是( )
A.①②B.①③C.②③④D.①③④
相关试题

