【题目】已知函数y=kx2+(2k+1)x+1(k为实数).
(1)对于任意实数k,函数图象一定经过点(﹣2,﹣1)和点_____;
(2)对于任意正实数k,当x>m时,y随着x的增大而增大,写出一个满足题意的m的值.
参考答案:
【答案】(1) (0,1);(2) 0.
【解析】
(1)分别将x取﹣2或0时,计算相应的函数值,即可得到答案;
(2)先由k>0,判断函数图象的开口方向,再求出函数的对称轴,则m>﹣1时均符合题意,任取范围内一个m值即可.
解:(1)∵y=kx2+(2k+1)x+1(k为实数).
∴当x=﹣2时,y=4k+(2k+1)×(﹣2)+1=1,
当x=0时,y=0+0+1=1,
∴对于任意实数k,函数图象一定经过点(﹣2,﹣1)和点 (0,1),
故答案为:(0,1);
(2)∵k为任意正整数,
∴k>0,
∴函数图象开口向上,
∵函数y=kx2+(2k+1)x+1的对称轴为![]() ,
,
∴在对称轴右侧,y随x的增大而增大,
∵x>m时,y随x的增大而增大,
∴![]() ,
,
故m=0时符合题意.(答案不唯一,m≥﹣1即可).
故答案为:0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2﹣2ax.
(1)二次函数图象的对称轴是直线x= ;
(2)当0≤x≤3时,y的最大值与最小值的差为4,求该二次函数的表达式;
(3)若a<0,对于二次函数图象上的两点P(x1,y1),Q(x2,y2),当t≤x1≤t+1,x2≥3时,均满足y1≥y2,请结合函数图象,直接写出t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=120°,点P为射线OA上一动点(不与点O重合),点C为∠AOB内部一点,连接CP,将线段CP绕点C顺时针旋转60°得到线段CQ,且点Q恰好落在射线OB上,不与点O重合.
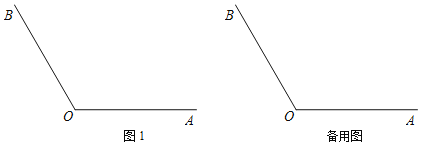
(1)依据题意补全图1;
(2)用等式表示∠CPO与∠CQO的数量关系,并证明;
(3)连接OC,写出一个OC的值,使得对于任意点P,总有OP+OQ=4,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个圆上所有的点都在一个角的内部或边上,那么称这个圆为该角的角内圆.特别地,当这个圆与角的至少一边相切时,称这个圆为该角的角内相切圆.在平面直角坐标系xOy中,点E,F分别在x轴的正半轴和y轴的正半轴上.
(1)分别以点A(1,0),B(1,1),C(3,2)为圆心,1为半径作圆,得到⊙A,⊙B和⊙C,其中是∠EOF的角内圆的是 ;
(2)如果以点D(t,2)为圆心,以1为半径的⊙D为∠EOF的角内圆,且与直线y=x有公共点,求t的取值范围;
(3)点M在第一象限内,如果存在一个半径为1且过点P(2,2
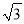 )的圆为∠EMO的角内相切圆,直接写出∠EOM的取值范围.
)的圆为∠EMO的角内相切圆,直接写出∠EOM的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 ,点
,点 在直线
在直线 上,以点
上,以点 为圆心,适当长度为半径画弧,分别交直线
为圆心,适当长度为半径画弧,分别交直线 ,
,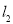 于
于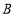 ,
,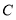 两点,以点
两点,以点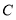 为圆心,
为圆心, 长为半径画弧,与前弧交于点
长为半径画弧,与前弧交于点 (不与点
(不与点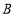 重合),连接
重合),连接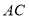 ,
,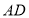 ,
, ,
,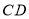 ,其中
,其中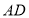 交
交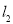 于点
于点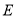 .若
.若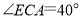 ,则下列结论错误的是( )
,则下列结论错误的是( )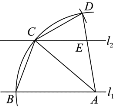
A.
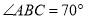 B.
B.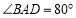 C.
C.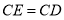 D.
D.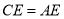
-
科目: 来源: 题型:
查看答案和解析>>【题目】生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的
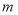 天数据,整理后绘制成统计表进行分析.
天数据,整理后绘制成统计表进行分析.日均可回收物回收量(千吨)
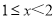
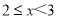

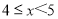
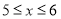
合计
频数
1
2
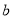
3
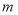
频率
0.05
0.10
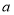
0.15
1
表中
 组的频率
组的频率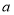 满足
满足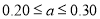 .
.下面有四个推断:
①表中
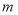 的值为20;
的值为20;②表中
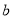 的值可以为7;
的值可以为7;③这
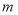 天的日均可回收物回收量的中位数在
天的日均可回收物回收量的中位数在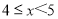 组;
组;④这
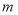 天的日均可回收物回收量的平均数不低于3.
天的日均可回收物回收量的平均数不低于3.所有合理推断的序号是( )
A.①②B.①③C.②③④D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地扶贫人员甲从办公室出发,骑车匀速前往所
 村走访群众,出发几分钟后,扶贫人员乙发现甲的手机落在办公室,无法联系,于是骑车沿相同的路线匀速去追甲.乙刚出发2分钟,甲也发现自己手机落在办公室,立刻原路原速骑车返回办公室,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回办公室,甲继续原路原速赶往
村走访群众,出发几分钟后,扶贫人员乙发现甲的手机落在办公室,无法联系,于是骑车沿相同的路线匀速去追甲.乙刚出发2分钟,甲也发现自己手机落在办公室,立刻原路原速骑车返回办公室,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回办公室,甲继续原路原速赶往 村.甲、乙两人相距的路程
村.甲、乙两人相距的路程 (米)与甲出发的时间
(米)与甲出发的时间 (分)之间的关系如图所示(乙给甲手机的时间忽略不计).有下列三个说法:
(分)之间的关系如图所示(乙给甲手机的时间忽略不计).有下列三个说法:
①甲出发10分钟后与乙相遇;
②甲的速度是400米/分;
③乙返回办公室用时4分钟.
其中所有正确说法的序号是_________.
相关试题

