【题目】如图,点C是以点O为圆心,AB为直径的半圆上的动点(不与点A,B重合),AB=6cm,过点C作CD⊥AB于点D,E是CD的中点,连接AE并延长交![]() 于点F,连接FD.小腾根据学习函数的经验,对线段AC,CD,FD的长度之间的关系进行了探究.
于点F,连接FD.小腾根据学习函数的经验,对线段AC,CD,FD的长度之间的关系进行了探究.

下面是小腾的探究过程,请补充完整:
(1)对于点C在![]() 上的不同位置,画图、测量,得到了线段AC,CD,FD的长度的几组值,如表:
上的不同位置,画图、测量,得到了线段AC,CD,FD的长度的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | |
AC/cm | 0.1 | 0.5 | 1.0 | 1.9 | 2.6 | 3.2 | 4.2 | 4.9 |
CD/cm | 0.1 | 0.5 | 1.0 | 1.8 | 2.2 | 2.5 | 2.3 | 1.0 |
FD/cm | 0.2 | 1.0 | 1.8 | 2.8 | 3.0 | 2.7 | 1.8 | 0.5 |
在AC,CD,FD的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;

(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解答问题:当CD>DF时,AC的长度的取值范围是 .
参考答案:
【答案】(1)AC,CD,FD;(2)详见解析;(3)3.5cm<x<5cm
【解析】
(1)根据函数的定义可得结论.
(2)利用描点法画出函数图象即可.
(3)利用图象法,观察图象写出函数CD的图象在函数DF的图象上方时,自变量的取值范围即可.
解:(1)由题意可知:AC是自变量,CD,DF是自变量AC的函数.
故答案为:AC,CD,FD.
(2)函数图象如图所示:
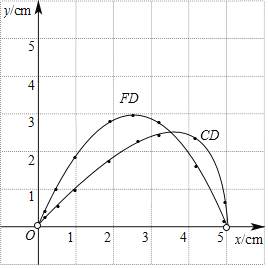
(3)观察图象可知CD>DF时,3.5cm<x<5cm.
故答案为:3.5cm<x<5cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AC,BD交于点O,且AO=BO.
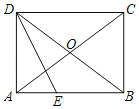
(1)求证:四边形ABCD是矩形;
(2)∠ADB的角平分线DE交AB于点E,当AD=3,tan∠CAB=
 时,求AE的长.
时,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】居民人均可支配收入、居民人均消费总支出和恩格尔系数都是反映居民生活水平的指标,其中恩格尔系数指居民家庭中食品支出占消费总支出的比重,恩格尔系数越小,说明食品支出占消费总支出比重越低,居民家庭越富裕,反之越贫穷.
下面是根据从权威机构获得的部分数据绘制的统计图:
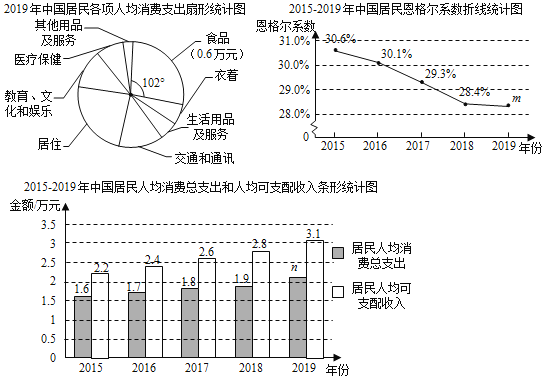
根据以上信息,回答下列问题:
(1)2019年中国城乡居民恩格尔系数m约为 (精确到0.1%);
(2)2019年居民人均消费总支出n约为 万元(精确到千位);
(3)下面的推断合理的是 .
①2015﹣2019年中国城乡居民人均可支配收入和人均消费总支出均呈逐年上升的趋势,说明中国居民生活水平逐步提高;
②2015﹣2019年中国城乡居民恩格尔系数呈现下降趋势,说明中国居民家庭富裕程度越来越高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠A=90°,∠B=22.5°,点P为线段BC上一动点,当点P运动到某一位置时,它到点A,B的距离都等于a,到点P的距离等于a的所有点组成的图形为W,点D为线段BC延长线上一点,且点D到点A的距离也等于a.
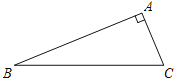
(1)求直线DA与图形W的公共点的个数;
(2)过点A作AE⊥BD交图形W于点E,EP的延长线交AB于点F,当a=2时,求线段EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2﹣2ax.
(1)二次函数图象的对称轴是直线x= ;
(2)当0≤x≤3时,y的最大值与最小值的差为4,求该二次函数的表达式;
(3)若a<0,对于二次函数图象上的两点P(x1,y1),Q(x2,y2),当t≤x1≤t+1,x2≥3时,均满足y1≥y2,请结合函数图象,直接写出t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=120°,点P为射线OA上一动点(不与点O重合),点C为∠AOB内部一点,连接CP,将线段CP绕点C顺时针旋转60°得到线段CQ,且点Q恰好落在射线OB上,不与点O重合.
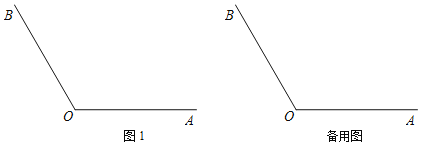
(1)依据题意补全图1;
(2)用等式表示∠CPO与∠CQO的数量关系,并证明;
(3)连接OC,写出一个OC的值,使得对于任意点P,总有OP+OQ=4,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个圆上所有的点都在一个角的内部或边上,那么称这个圆为该角的角内圆.特别地,当这个圆与角的至少一边相切时,称这个圆为该角的角内相切圆.在平面直角坐标系xOy中,点E,F分别在x轴的正半轴和y轴的正半轴上.
(1)分别以点A(1,0),B(1,1),C(3,2)为圆心,1为半径作圆,得到⊙A,⊙B和⊙C,其中是∠EOF的角内圆的是 ;
(2)如果以点D(t,2)为圆心,以1为半径的⊙D为∠EOF的角内圆,且与直线y=x有公共点,求t的取值范围;
(3)点M在第一象限内,如果存在一个半径为1且过点P(2,2
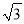 )的圆为∠EMO的角内相切圆,直接写出∠EOM的取值范围.
)的圆为∠EMO的角内相切圆,直接写出∠EOM的取值范围.
相关试题

