【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A![]() B
B![]() C
C![]() .
.
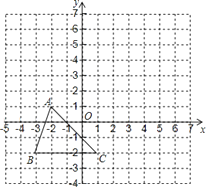
(1)在图中画出△A![]() B
B![]() C
C![]() ;
;
(2)写出点A![]() 、B
、B![]() 、C
、C![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在一点P,使得△PBC与△ABC面积相等?若存在,写出点P的坐标;若不存在,说明理由.
轴上是否存在一点P,使得△PBC与△ABC面积相等?若存在,写出点P的坐标;若不存在,说明理由.
参考答案:
【答案】(1)见解析;(2)A′(0,4),B′(-1,1),C′(3,1);(3)存在,点P的坐标是(0,1)或(0,-5).
【解析】
(1)分别把A,B,C三点向上平移3个单位长度,再向右平移2个单位长度即得A′,B′,C′三点连线即可;(2)可以先写出A,B,C三点坐标,然后分别把各点的横坐标加2,纵坐标加3即得A′,B′,C′坐标;(3)先把△ABC面积求出来,S△ABC=4×3÷2=6,若存在,设P点到BC的距离为x,BC=4,当△PBC与△ABC面积相等时,4x÷2=6,x=3,P点到BC的距离为3的点有2个为±3,当为3时,P点纵坐标是3-2=1,当为-3时,P点纵坐标是-3-2=-5,综上所述,y轴上存在点P,使得△PBC与△ABC面积相等,点P的坐标是(0,1)或(0,-5).
解:(1)分别把A,B,C三点向上平移3个单位长度,再向右平移2个单位长度即得A′,B′,C′,画出三角形A′B′C′;如图:
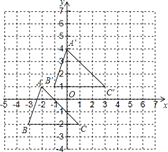
(2)由图写出A,B,C三点坐标:A(-2,1),B(-3,-2),C(1,-2),
∵上平移3个单位长度,右平移2个单位长度,
∴各点的横坐标加2,纵坐标加3得,:A′(0,4),B′(-1,1),C′(3,1).
(3)由图可知,S△ABC=4×3÷2=6,BC=4,设P点到BC的距离为x,4x÷2=6,x=3,
∵P点到BC的距离为3的点有2个为±3,
∴当为3时,P点纵坐标是3-2=1,当为-3时,P点纵坐标是-3-2=-5,P点横坐标是0,
∴点P的坐标是(0,1)或(0,-5).
-
科目: 来源: 题型:
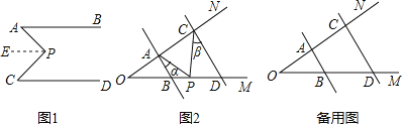
查看答案和解析>>【题目】(1)如图1,AB∥CD,∠A=38°,∠C=50°,求∠APC的度数.(提示:作PE∥AB).
(2)如图2,AB∥DC,当点P在线段BD上运动时,∠BAP=∠α,∠DCP=∠β,求∠CPA与∠α,∠β之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点P在段线OB上运动,请你直接写出∠CPA与∠α,∠β之间的数量关系______.
-
科目: 来源: 题型:
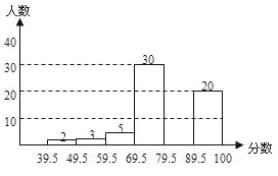
查看答案和解析>>【题目】我市今年九年级体育考试结束后,从某县3000名参考学生中抽取了100名考生成绩进行统计分析(满分100分,记分均为整数),得到如图所示的频数分布直方图,请你根据图形完成下列问题:
(1)本次抽样的样本容量是_________
(2)请补全频数分布直方图.
(3)若80分以上(含80分)为优秀,请你据此估算该县本次考试的优秀人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个足球和3个篮球共需340元,购买5个足球和2个篮球共需410元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据学校的实际情况,需购买足球和篮球共96个,并且总费用不超过5720元.问最多可以购买多少个篮球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是( )
A.
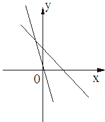 B.
B. 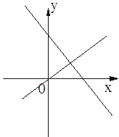
C.
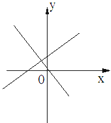 D.
D. 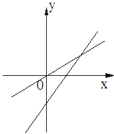
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知1+2+1=4=22,1+2+3+2+1=9=32,1+2+3+4+3+2+1=16=42,1+2+3+4+5+4+3+2+1=25=52.根据上面四式的计算规律求:1+2+3+…+2014+2015+2016+2015+2014+…+3+2+1=________(写出某数的平方即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】认真阅读并填空:
已知:如图,∠1=∠2,∠C=∠D,试说明:∠A=∠F.

解:∵∠1=∠2(已知),∠2=∠3( )
∴∠1=∠3(等量代换)
∴BD∥EC( )
∴∠4=∠C(两直线平行,同位角相等)
又∠C=∠D(已知)
∴∠4=∠D( )
∴ ∥ (内错角相等,两直线平行)
∴∠A=∠F( )
相关试题

