【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
(1)求证:AD=AN;
(2)若AB=8,ON=1,求⊙O的半径.

参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)先根据圆周角定理得出∠BAD=∠BCD,再由直角三角形的性质得出∠ANE=∠CNM,故可得出∠BCD=∠BAM,由全等三角形的判定定理得出△ANE≌△ADE,故可得出结论;
(2)先根据垂径定理求出AE的长,设NE=x,则OE=x-1,NE=ED=x,r=OD=OE+ED=2x-1
连结AO,则AO=OD=2x-1,在Rt△AOE中根据勾股定理可得出x的值,进而得出结论.
试题解析:
(1)证明:∵CD⊥AB
∴∠CEB=90
∴∠C+∠B=90.
同理∠C+∠CNM=90
∴∠CNM=∠B.
∵∠CNM=∠AND
∴∠AND=∠B
∵弧AC=弧AC
∴∠D=∠B
∴∠AND=∠D
∴AN=AD
(2)解:设ON的长为![]() ,连接OA
,连接OA
∵AN=AD,CD⊥AB
∴DE=NE= ![]()
∴OD=OE+ED= ![]()
∴OA=OD![]() .
.
∴在Rt△OAE中![]()
∴![]()
解得![]() 或
或![]() (不合题意,舍去).
(不合题意,舍去).
∴OA![]() .
.
即⊙O的半径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用因式分解计算:2012-1992=_________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的圆心角是( )
A.30°B.60°C.90°D.180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式
(1)20a3-30a2
(2)25(x+y)2-9(x-y)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE,BE,BE⊥AE,延长AE交BC的延长线于点F.求证:
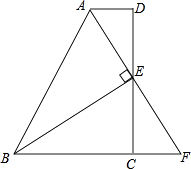
(1)FC=AD;
(2)AB=BC+AD. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,D是BC边的中点,E是AB延长线上的一点,且BE=BD,过点D作DH⊥AB于H.
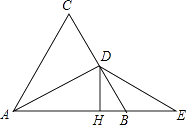
(1)求∠BAD和∠BDE的度数;
(2)求证:点H是AE的中点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=3,求6x2+4x﹣2(x2﹣1)﹣2(2x+x2)的值,小民粗心把x=3抄成了x=﹣3,但计算的结果却正确的.你知道其中的原因吗?
相关试题

