【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE,BE,BE⊥AE,延长AE交BC的延长线于点F.求证: 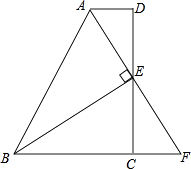
(1)FC=AD;
(2)AB=BC+AD.
参考答案:
【答案】
(1)证明:∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,
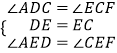 ,
,
∴△ADE≌△FCE(ASA),
∴FC=AD(全等三角形的性质)
(2)证明:∵△ADE≌△FCE,
∴AE=EF,AD=CF(全等三角形的对应边相等),
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF,
∵AD=CF(已证),
∴AB=BC+AD(等量代换)
【解析】(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答.(2)根据线段垂直平分线的性质判断出AB=BF即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的圆心角是( )
A.30°B.60°C.90°D.180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式
(1)20a3-30a2
(2)25(x+y)2-9(x-y)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
(1)求证:AD=AN;
(2)若AB=8,ON=1,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,D是BC边的中点,E是AB延长线上的一点,且BE=BD,过点D作DH⊥AB于H.
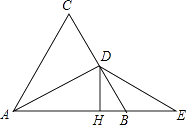
(1)求∠BAD和∠BDE的度数;
(2)求证:点H是AE的中点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=3,求6x2+4x﹣2(x2﹣1)﹣2(2x+x2)的值,小民粗心把x=3抄成了x=﹣3,但计算的结果却正确的.你知道其中的原因吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】据襄阳新闻报道2016年3月至2016年10月,襄阳闸口二路“大虾一条街”共销售大虾6000余吨.2017年潜江养虾专业户张小花抓住商机,将自己养殖的大虾销往襄阳.计算了养殖成本以及运费等诸多因素,他发现大虾的成本价为20元/公斤.经过市场调查,一周的销售量
 公斤与销售单价
公斤与销售单价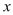 (
(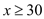 )元/公斤的关系如下表:
)元/公斤的关系如下表:销售单价
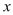 元/公斤
元/公斤...
30
35
40
45
...
销售量
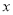 公斤
公斤...
500
450
400
350
...
(1)直接写出y与x的函数关系式;
(2)若张小花一周的销售利润为W元,请求出W与
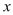 的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?(3)随着赚的钱越来越多,张小花决定回馈社会将一周的销售利润全部捐给襄阳市福利院.若一周张小花的总成本不超过4000元,请求出张小花最大捐款数额是多少元?
相关试题

