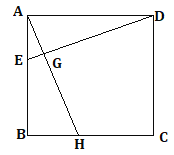
【题目】如图,点E、H分别在正方形ABCD的边AB、BC上,且AE=BH
求证:(1)DE=AH (2)DE⊥AH
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】(1)根据正方形的性质可得AD=AB, ∠DAE=∠ABC,然后利用“边角边”证明△AD和△BHA全等,根据全等三角形对应边相等可得DE=AH;
(2)根据全等三角形对应角相等可得∴∠EDA=∠HAB,然后求出∠EDA+∠HAD =∠DAE=90°,判断出AH⊥DE.
(1)∵四边形ABCD是正方形,
∴AD=AB, ∠DAE=∠ABC,
∵AE=BH
∴△AED≌△BHA(SAS)
∴DE=AH
(2) ∵△AED≌△BHA
∴∠EDA=∠HAB
∵∠HAB+∠HAD=90°
∴∠EDA+∠HAD=90°
∴DE⊥AH
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A,B两点,分别代表﹣40,20,两只电子蚂蚁甲,乙分别从AB两点同时出发,甲沿线段AB以3个单位长度/秒的速度向右运动,甲到达点B处时运动停止,乙沿BA方向以5个单位长度/秒的速度向左运动.

(1)A,B两点间的距离为 个单位长度;甲到达B点时共运动了 秒.
(2)甲,乙在数轴上的哪个点相遇?
(3)多少秒时,甲、乙相距28个单位长度?
(4)若乙到达A点后立刻掉头并保持速度不变,则甲到达B点前,甲,乙还能在数轴上相遇吗?若能,求出相遇点所对应的数;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连接对角线互相垂直的四边形的各边中点,所得图形一定是( )
A. 正方形 B. 菱形 C. 矩形 D. 梯形
-
科目: 来源: 题型:
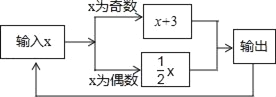
查看答案和解析>>【题目】有一数值转换器,原理如图所示,
(1)如果开始输入x的值是1,可发现第一次输出的是4,第二次输出的是 ,第三次输出的是 ,第4次输出的是 …,请根据你的发现填写如表:
输出次数
1
2
3
4
5
…
3n
3n+1
3n+2
输出的数
4
1
…
(2)如果开始输入的数是11,可发现第一次输出的是14,第二次输出的是7,…“,请你探索第2017次和2018次输出的结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC与正方形ODEF是位似图形,O为位似中心,相似比为1:
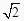 ,点A的坐标为(1,0),则E点的坐标为( )
,点A的坐标为(1,0),则E点的坐标为( ) 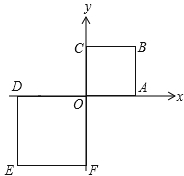
A.(-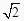 ,0)
,0)
B.(-1.5,-1.5)
C.(-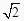 ,-
,- 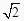 )
)
D.(-2,-2) -
科目: 来源: 题型:
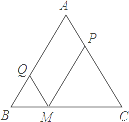
查看答案和解析>>【题目】已知:△ABC中AB=AC,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
探究:(1)线段QM、PM、AB之间有什么关系?并说明你的理由.
(2)当M位于BC的什么位置时, 四边形AQMP是菱形?并说明你的理由.
(3)当△ABC满足什么条件菱形AQMP是正方形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设实数a,b,c满足a>b>c(ac<0),且|c|<|b|<|a|,则|x-a|+|x+b|+|x-c|的最小值为( )
A.
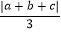 B. |b| C. a+b D. -c-a
B. |b| C. a+b D. -c-a
相关试题

