【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标;
(3)在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、G为顶点的四边形是正方形时,请求出点M的坐标.
参考答案:
【答案】
(1)
解:∵抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,
∴ ![]() ,
,
解得, ![]() ,
,
∴经过A,B,C三点的抛物线的函数表达式为y=﹣x2+2x+3
(2)
解:如图1 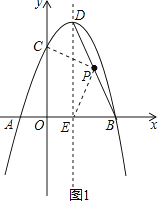 ,连接PC、PE,
,连接PC、PE,
x=﹣ ![]() =﹣
=﹣ ![]() =1,
=1,
当x=1时,y=4,
∴点D的坐标为(1,4),
设直线BD的解析式为:y=mx+n,
则 ![]() ,
,
解得, ![]() ,
,
∴直线BD的解析式为y=﹣2x+6,
设点P的坐标为(x,﹣2x+6),
则PC2=x2+(3+2x﹣6)2,PE2=(x﹣1)2+(﹣2x+6)2,
∵PC=PE,
∴x2+(3+2x﹣6)2=(x﹣1)2+(﹣2x+6)2,
解得,x=2,
则y=﹣2×2+6=2,
∴点P的坐标为(2,2);
(3)
解:设点M的坐标为(a,0),则点G的坐标为(a,﹣a2+2a+3),
∵以F、M、G为顶点的四边形是正方形,
∴FM=MG,即|2﹣a|=|﹣a2+2a+3|,
当2﹣a=﹣a2+2a+3时,
整理得,a2﹣3a﹣1=0,
解得,a= ![]() ,
,
当2﹣a=﹣(﹣a2+2a+3)时,
整理得,a2﹣a﹣5=0,
解得,a= ![]() ,
,
∴当以F、M、G为顶点的四边形是正方形时,点M的坐标为( ![]() ,0),(
,0),( ![]() ,0),(
,0),( ![]() ,0),(
,0),( ![]() ,0)
,0)
【解析】(1)利用待定系数法求出过A,B,C三点的抛物线的函数表达式;
(2)连接PC、PE,利用公式求出顶点D的坐标,利用待定系数法求出直线BD的解析式,设出点P的坐标为(x,﹣2x+6),利用勾股定理表示出PC2和PE2 , 根据题意列出方程,解方程求出x的值,计算求出点P的坐标;
(3)设点M的坐标为(a,0),表示出点G的坐标,根据正方形的性质列出方程,解方程即可.本题考查的是二次函数的图象和性质、待定系数法求函数解析式以及正方形的性质,掌握二次函数的图象和性质、灵活运用待定系数法是解题的关键.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D,CE是△ABC的角平分线.
(1)求∠DCE的度数.
(2)若∠CEF=135°,求证:EF∥BC.

-
科目: 来源: 题型:
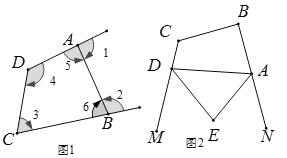
查看答案和解析>>【题目】(1)如图1,试探究其中∠1,∠2与∠3,∠4之间的关系,并证明.
(2)用(1)中的结论解决下列问题:如图2,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=
 ∠A.
∠A. 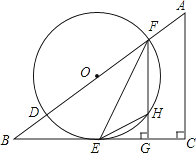
(1)求证:BC是⊙O的切线;
(2)若sinB=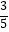 ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,D1是△ABC的边AB上的一点,则图中有哪几个三角形?
(2)如图2,D1,D2是△ABC的边AB上的两点,则图中有哪几个三角形?
(3)如图3,D1,D2,…,D10是△ABC的边AB上的10个点,则图中共有多少个三角形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2 , 求原正方形空地的边长.设原正方形的空地的边长为xm,则可列方程为( )
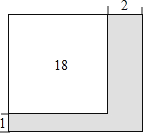
A.(x+1)(x+2)=18
B.x2﹣3x+16=0
C.(x﹣1)(x﹣2)=18
D.x2+3x+16=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由下列条件可判定哪两条直线平行,并说明根据.
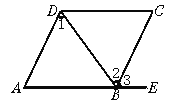
(1)∠1=∠2,________________________.
(2)∠A=∠3,________________________.
(3)∠ABC+∠C=180°,________________________.
相关试题

