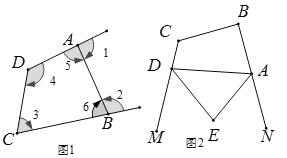
【题目】(1)如图1,试探究其中∠1,∠2与∠3,∠4之间的关系,并证明.
(2)用(1)中的结论解决下列问题:如图2,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
参考答案:
【答案】(1)∠1+∠2=∠3+∠4(2)60°
【解析】
(1)由四边形的内角和是360°,以及邻补角的和是180°求解即可;
(2)依据(1)的结论可知∠MDA+∠DAN=240°,由角平分线的定义可求得∠EDA+∠EAD=120°,最后在△ADE中由勾股定理可求得∠E的度数.
(1)∠1+∠2=∠3+∠4,理由如下:
由四边形的内角和是360°可知:∠3+∠4+∠5+∠6=360°,
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2+∠5+∠6=360°,
∴∠1+∠2=∠3+∠4;
(2)由(1)可知∠MDA+∠DAN=∠B+∠C=240°,
∵AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,
∴∠EDA=![]() ∠MDA,∠EAD=
∠MDA,∠EAD=![]() ∠DAN,
∠DAN,
∴∠EDA+∠EAD=![]() ×(∠MDA+∠DAN)=
×(∠MDA+∠DAN)=![]() ×240°=120°,
×240°=120°,
∴∠E=180°-(∠EDA+∠EAD) =180°-120°=60°.
-
科目: 来源: 题型:
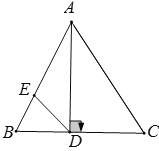
查看答案和解析>>【题目】如图所示,在△ABC中,已知AD⊥BC,∠B=64°,∠C=56°,
(1)求∠BAD和∠DAC的度数;
(2)若DE平分∠ADB,求∠AED的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
“读书节”活动计划书
书本类别
A类
B类
进价(单位:元)
18
12
备注
1、用不超过16800元购进A、B两类图书共1000本;
2、A类图书不少于600本;
…
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买的图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A、B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润? -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D,CE是△ABC的角平分线.
(1)求∠DCE的度数.
(2)若∠CEF=135°,求证:EF∥BC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=
 ∠A.
∠A. 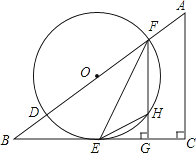
(1)求证:BC是⊙O的切线;
(2)若sinB=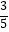 ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.

(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标;
(3)在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、G为顶点的四边形是正方形时,请求出点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,D1是△ABC的边AB上的一点,则图中有哪几个三角形?
(2)如图2,D1,D2是△ABC的边AB上的两点,则图中有哪几个三角形?
(3)如图3,D1,D2,…,D10是△ABC的边AB上的10个点,则图中共有多少个三角形?

相关试题

