【题目】如图,由下列条件可判定哪两条直线平行,并说明根据.
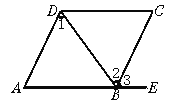
(1)∠1=∠2,________________________.
(2)∠A=∠3,________________________.
(3)∠ABC+∠C=180°,________________________.
参考答案:
【答案】AD∥BC,内错角相等,两直线平行 AD∥BC,同位角相等,两直线平行 AB∥CD,同旁内角互补,两直线平行
【解析】
(1)根据内错角相等,两直线平行推出即可;
(2)根据同位角相等,两直线平行推出即可;
(3)根据同旁内角互补,两直线平行推出即可.
解(1)∵∠1=∠2,
∴AD∥BC(内错角相等,两直线平行),
故答案为:AD∥BC,根据内错角相等,两直线平行;
(2)∵∠A=∠3,
∴AD∥BC(同位角相等,两直线平行),
故答案为:AD∥BC,根据同位角相等,两直线平行;
(3)∵∠ABC+∠C=180°,
∴AB∥CD(同旁内角互补,两直线平行),
故答案为:AB∥CD,根据同旁内角互补,两直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.

(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标;
(3)在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、G为顶点的四边形是正方形时,请求出点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,D1是△ABC的边AB上的一点,则图中有哪几个三角形?
(2)如图2,D1,D2是△ABC的边AB上的两点,则图中有哪几个三角形?
(3)如图3,D1,D2,…,D10是△ABC的边AB上的10个点,则图中共有多少个三角形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2 , 求原正方形空地的边长.设原正方形的空地的边长为xm,则可列方程为( )
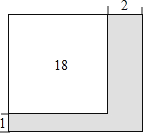
A.(x+1)(x+2)=18
B.x2﹣3x+16=0
C.(x﹣1)(x﹣2)=18
D.x2+3x+16=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
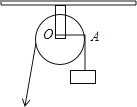
A.πcm
B.2πcm
C.3πcm
D.5πcm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】填写理由:
已知:如图,ABC是直线,∠1=115°,∠D=65°.
求证:AB∥DE.
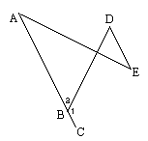
证明:∵ABC是一直线,(已知)
∴∠1+∠2=180°( )
∵∠1=115°(已知)
∴∠2=65°
又∵∠D=65°(已知)
∴∠2=∠D
∴ ∥ ( )
相关试题

