搜索
【题目】一次函数y=ax+b（a≠0）与二次函数y=ax2+2x+b（a≠0）在同一直角坐标系中的图象可能是（ ）
A.
B.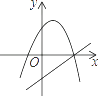
C.
D.
参考答案：
【答案】D
【解析】解：A、由抛物线可知，a＞0，得b＞0，由直线可知，a＜0，b＞0，故本选项错误；
B、由抛物线可知，a＜0，b＞0，由直线可知，a＞0，b＜0，故本选项错误；
C、由抛物线可知，a＜0，b＞0，由直线可知，a＜0，b＜0，故本选项错误；
D、由抛物线可知，a＞0，b＞0，由直线可知，a＞0，b＞0，且交y轴同一点，故本选项正确．
所以答案是：D．
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识，掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
-
科目： 来源： 题型：
查看答案和解析>>【题目】永州市在进行“六城同创”的过程中,决定购买
两种树对某路段进行绿化改造,若购买
种树2棵, 
种树3棵,需要2700元；购买种树4棵, 种树5棵,需要4800元.(1)求购买
两种树每棵各需多少元?(2)考虑到绿化效果,购进A种树不能少于48棵,且用于购买这两种树的资金不低于52500元.若购进这两种树共100棵.问有哪几种购买方案?
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线
经过 
两点．
（1）求抛物线的解析式和顶点坐标；
（2）设点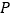
为抛物线上一点，若 
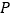，求点 的坐标． -
科目： 来源： 题型：
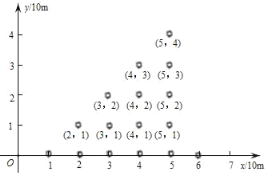
查看答案和解析>>【题目】某景区有一片树林，不仅树种相同，而且排列有序，如果用平面直角坐标系来表示每一棵的具体位置，从第一棵树开始依次表示为（1，0）→（2，0）→（2，1）→（3，2）→（3，1）→（3，0）→（4.0）→……，则第100棵树的位置是____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图，有下列5个结论：
①abc＜0；②3a+c＞0；③4a+2b+c＞0；④2a+b=0；⑤b2＞4ac．
其中正确的结论的有（ ）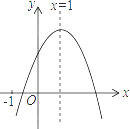
A.2个
B.3个
C.4个
D.5个 -
科目： 来源： 题型：
查看答案和解析>>【题目】某同学用10×10的方形网格绘制了遵义市四所初级中学（黑色格点）的位置图．（平方单位）
（1）请在适当的位置建立平面直角坐标系，并根据该平面直角坐标系解答下列问题；
（2）分别写出四所中学所在位置的坐标：一中 ，二中 ，三中 ，四中 ；
（3）分别记一中A、二中B、四中C，移动“三中”的位置于点D（请自行在图中标记），连接A、B、C、D四点组成的四边形ABCD为平行四边形．
①移动后所得D点的坐标是 （写一个点）；
②求所得平行四边形ABCD的面积．
-
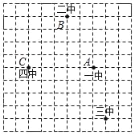
科目： 来源： 题型：
查看答案和解析>>【题目】如图1,在
和
中, 
,
,
.
(1)若
三点在同一直线上,连接
交
于点
,求证: 
.(2)在第(1)问的条件下,求证:
；(3)将
绕点
顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由.
相关试题
