Question

【题目】如图，矩形ABCD中，AB=6，BC=8，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处，当△CEB′为直角三角形时，BE的长为 ．

Answer 1

【答案】3或6
【解析】解：当△CEB′为直角三角形时，有两种情况：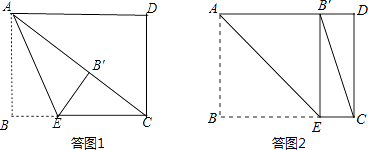
①当点B′落在矩形内部时，如答图1所示．
连结AC，
在Rt△ABC中，AB=6，BC=8，
∴AC= =10，
∵∠B沿AE折叠，使点B落在点B′处，
∴∠AB′E=∠B=90°，
当△CEB′为直角三角形时，只能得到∠EB′C=90°，
∴点A、B′、C共线，即∠B沿AE折叠，使点B落在对角线AC上的点B′处，如图，
∴EB=EB′，AB=AB′=6，
∴CB′=10﹣6=4，
设BE=x，则EB′=x，CE=8﹣x，
在Rt△CEB′中，
∵EB′2+CB′2=CE2 ，
∴x2+42=（8﹣x）2 ，
解得x=3，
∴BE=3；
②当点B′落在AD边上时，如答图2所示．
此时ABEB′为正方形，
∴BE=AB=6．
综上所述，BE的长为3或6．
故答案为：3或6．
当△CEB′为直角三角形时，有两种情况：
①当点B′落在矩形内部时，如答图1所示．
连结AC，先利用勾股定理计算出AC=10，根据折叠的性质得∠AB′E=∠B=90°，而当△CEB′为直角三角形时，只能得到∠EB′C=90°，所以点A、B′、C共线，即∠B沿AE折叠，使点B落在对角线AC上的点B′处，则EB=EB′，AB=AB′=6，可计算出CB′=4，设BE=x，则EB′=x，CE=8﹣x，然后在Rt△CEB′中运用勾股定理可计算出x．
②当点B′落在AD边上时，如答图2所示．此时四边形ABEB′为正方形．