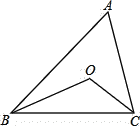
【题目】如图,在![]() ABC中,BO、CO分别平分∠ABC和∠ACB.计算:
ABC中,BO、CO分别平分∠ABC和∠ACB.计算:
(1)若∠A ![]() 60°,求∠BOC的度数;
60°,求∠BOC的度数;
(2)若∠A ![]() 100°, 则∠BOC的度数是多少?
100°, 则∠BOC的度数是多少?
(3)若∠A ![]() 120°, 则∠BOC的度数又是多少?
120°, 则∠BOC的度数又是多少?
(4)由(1)、(2)、(3),你发现了什么规律?请用一个等式将这个规律表示出来.
参考答案:
【答案】(1)∠BOC![]() 120°;(2)∠BOC
120°;(2)∠BOC![]() 140°;(3)∠BOC=150°;(4)∠BOC=90°+
140°;(3)∠BOC=150°;(4)∠BOC=90°+![]() ∠A
∠A
【解析】
(1)根据BO、CO分别平分∠ABC和∠ACB可得: ∠CBO+∠BCO的值,再根据三角形内角和得出∠BOC;
(2)、(3)同理(1)可求得;
(4)根据(1)-(3)规律可得.
(1)∵BO、CO分别平分∠ABC和∠ACB.∠A ![]() 600
600
∴∠CBO+∠BCO![]()
![]() (1800
(1800![]() ∠A)
∠A)![]()
![]() (1800
(1800![]() 600)
600)![]() 600
600
∴∠BOC![]() 1800
1800![]() (∠CBO+∠BCO)
(∠CBO+∠BCO)![]() 1800
1800![]() 600
600![]() 1200
1200
(2)同理,若∠A ![]() 1000, 则∠BOC
1000, 则∠BOC![]() 1800
1800![]()
![]() (1800
(1800![]() ∠A)
∠A)![]() 900+
900+![]() ∠A
∠A![]() 140
140
(3)同理,若∠A ![]() 1200, 则∠BOC
1200, 则∠BOC![]() 1800
1800![]()
![]() (1800
(1800![]() ∠A)
∠A)![]() 900+
900+![]() ∠A
∠A![]() 1500
1500
(4)由(1)、(2)、(3),发现:∠BOC![]() 1800
1800![]()
![]() (1800
(1800![]() ∠A)
∠A)![]() 900+
900+![]() ∠A
∠A
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )

A.2
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半.
(1)求这个多边形是几边形;
(2)求这个多边形的每一个内角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AD⊥BC,垂足为点D,DE∥AC交AB于E,DF∥AB交AC于F,当△ABC再添加一个条件:时,四边形AEDF为菱形(填写一个条件即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE. 求证:四边形BCDE是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两张宽为1cm的矩形纸条交叉叠放,其中重叠部分部分是四边形ABCD,

(1)试判断四边形ABCD的形状,并说明理由
(2)若∠BAD=30°,求重叠部分的面积.
相关试题

