搜索
【题目】如图，在矩形纸片ABCD中，AB=2，AD=3，点E是AB的中点，点F是AD边上的一个动点，将△AEF沿EF所在直线翻折，得到△A′EF，则A′C的长的最小值是 ．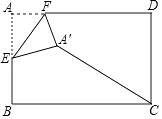 
参考答案：
【答案】
﹣1
【解析】解：连接CE，如图所示．
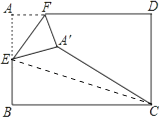
根据折叠可知：A′E=AE= 
AB=1．
在Rt△BCE中，BE= AB=1，BC=3，∠B=90°，
∴CE= 
= ．
∵CE= ，A′E=1，
∴点A′在CE上时，A′C取最小值，最小值为CE﹣A′E= ﹣1．
所以答案是： ﹣1．
【考点精析】认真审题，首先需要了解矩形的性质(矩形的四个角都是直角，矩形的对角线相等)，还要掌握翻折变换（折叠问题）(折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等)的相关知识才是答题的关键．
-
科目： 来源： 题型：
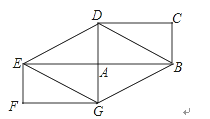
查看答案和解析>>【题目】如图，矩形ABCD和矩形AEFG关于点A中心对称，
（1）四边形BDEG是菱形吗？请说明理由．
（2）若矩形ABCD面积为8，求四边形BDEG的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的边长为8，在各边上顺次截取AE=BF=CG=DH=5，则四边形EFGH的面积是（ ）
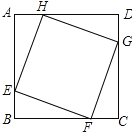
A. 30 B. 34 C. 36 D. 40
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，对角线AC的垂直平分线分别交AD，BC于点E，F，连接CE，若△CED的周长为6，则ABCD的周长为（ ）
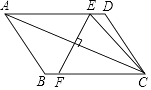
A.6
B.12
C.18
D.24 -
科目： 来源： 题型：
查看答案和解析>>【题目】在下列说法中：①过一点有且只有一条直线与已知直线平行；②-0.9是0.81的平方根；③若在平面直角坐标系中直线
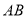垂直于
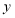轴，则直线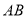上所有的点的横坐标相同；④
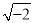是一个负数；⑤0的相反数和倒数都是0；⑥
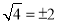；⑦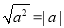
；⑧全体有理数和数轴上的点一一对应．以上真命题的序号是__________． -
科目： 来源： 题型：
查看答案和解析>>【题目】为保护美丽如画的邛海湿地，西昌市污水处理厂决定先购买
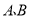两型污水处理设备共20台，对湿地周边污水进行处理．每台
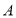型污水处理设备12万，每台
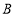型污水处理设备10万，已知2台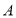型污水处理设备和1台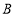型污水处理设备每周处理污水680吨，3台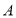型污水处理设备和2台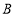型污水处理设备每周处理污水1120吨．（1）求每台
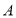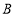、型污水处理设备每周分别可以处理污水多少吨？（2）经预算，污水处理厂购买设备的资金不超过230万元，每周处理污水的量不低于4500吨，请列举出所有购买方案，并指出所需购买资金最少的方案及最少资金．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们知道，经过原点的抛物线可以用y=ax2+bx（a≠0）表示，对于这样的抛物线：
（1）当抛物线经过点（﹣2，0）和（﹣1，3）时，求抛物线的表达式；
（2）当抛物线的顶点在直线y=﹣2x上时，求b的值；
（3）如图，现有一组这样的抛物线，它们的顶点A1、A2、…，An在直线y=﹣2x上，横坐标依次为﹣1，﹣2，﹣3，…，﹣n（n为正整数，且n≤12），分别过每个顶点作x轴的垂线，垂足记为B1、B2 ， …，Bn ， 以线段AnBn为边向左作正方形AnBnCnDn ， 如果这组抛物线中的某一条经过点Dn ， 求此时满足条件的正方形AnBnCnDn的边长．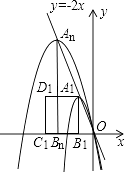
相关试题
