【题目】如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
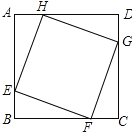
A. 30 B. 34 C. 36 D. 40
参考答案:
【答案】B
【解析】在Rt△AEH中,由勾股定理求出EH=![]() ,根据正方形面积公式求出即可
,根据正方形面积公式求出即可
解: ∵四边形ABCD是正方形, AE=BF=CG=DH, ∴AH=DG=CF=BE,
∴△AEH≌△DHG≌△CGF≌△BFE(SAS),
∴EH=EF=FG=HG,∵∠A=∠D=90°,
∴∠DGH+∠DHG=90°,
∴∠AHE+∠DHG=90°,
∴∠EHG=180°-90°=90°,
∴四边形EFGH是正方形,
在Rt△AEH中,AE=2,AH=5,由勾股定理得:EH=![]() =
=![]() ,
,
∵四边形EFGH是正方形,
∴EF=FG=GH=EH=![]() ,
,
∴四边形EFGH的面积是(![]() )2=34.
)2=34.
故选B.
“点睛”本题考查了正方形性质,全等三角形的性质和判定,三角形内角和定理,正方形判定的应用,关键是推出四边形EFGH是正方形.
-
科目: 来源: 题型:
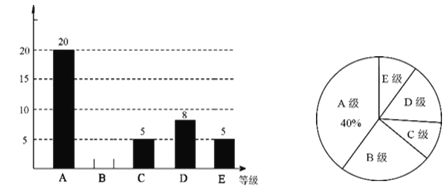
查看答案和解析>>【题目】为了强化同学们的校园安全意识,某学校组织全校3000名同学参加校园安全知识测试,成绩记为A,B,C,D,E共5个等级,为了解本次测试的成绩(等级)情况,现从中随机抽取部分同学的成绩(等级),统计整理并制作了如下的统计图:
(1)求这次抽样调查的样本容量是 ;
(2)请补全条形统计图;
(3)如果测试成绩(等级)为A,B,C级的定为优秀,请估计该学校参加本次校园安全知识测试成绩(等级)达到优秀的同学的总人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一组数1,3,5,7,9,…,按此规律,则第n个数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列图形的排列规律(其中☆,□,●分别表示五角星、正方形、圆).
●□☆●●□☆●□☆●●□☆●……
若第一个图形是圆,则第2018个图形是__________(填名称).
-
科目: 来源: 题型:
查看答案和解析>>【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a.
如:1☆3=1×32+2×1×3+1=16.
(1)求(﹣2)☆3的值;
(2)若(
 ☆3)☆(﹣
☆3)☆(﹣ )=8,求a的值;
)=8,求a的值;(3)若2☆x=m,(
 x)☆3=n(其中x为有理数),试比较m,n的大小.
x)☆3=n(其中x为有理数),试比较m,n的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】70°30′的余角为°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个正方形截去(至少)一个角,则其边数_______.
相关试题

