【题目】问题背景:
如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC、CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.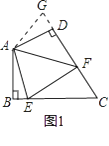
(1)小明同学探究此问题的方法是,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;
(2)探索延伸:
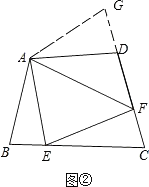
如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF= ![]() ∠BAD,上述结论是否仍然成立,请说明理由;
∠BAD,上述结论是否仍然成立,请说明理由; 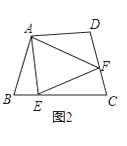
(3)实际应用:
如图③,在某次军事演习中,舰艇甲在指挥中心O北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,当∠EOF=70°时,两舰艇之间的距离是海里.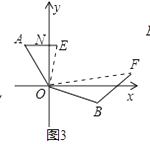
(4)能力提高:
如图④,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为 . 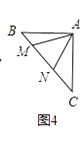
参考答案:
【答案】
(1)EF=BE+DF
(2)
解:结论EF=BE+DF仍然成立;
理由:延长FD到点G.使DG=BE.连结AG,如图②,
在△ABE和△ADG中, 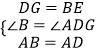 ,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF= ![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中, 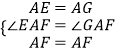 ,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
(3)280
(4)![]()
【解析】解:(1.)EF=BE+DF,证明如下:
在△ABE和△ADG中, 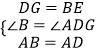 ,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF= ![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中, 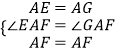 ,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
所以答案是 EF=BE+DF.
(3.)如图③,连接EF,延长AE、BF相交于点C,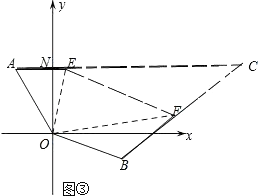
∵∠AOB=30°+90°+(90°﹣70°)=140°,∠EOF=70°,
∴∠EOF= ![]() ∠AOB,
∠AOB,
又∵OA=OB,∠OAC+∠OBC=(90°﹣30°)+(70°+50°)=180°,
∴符合探索延伸中的条件,
∴结论EF=AE+BF成立,
即EF=2×(60+80)=280海里.
答:此时两舰艇之间的距离是280海里;
所以答案是:280;
(4.)如图4,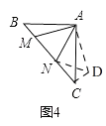
将△ABM绕点A逆时针旋转得到△ACD,
∴△ABM≌△ACD,
∴∠AMB=∠ADC,∠BAM=∠CAM,AM=AD,BM=CD=1,
∵∠AMB+∠AMC=90°,
∴∠AMC+∠ADC=180°,
∴∠MAD+∠MCD=180°,
∵∠BAC=90°,
∴∠MAD=∠MAC+∠CAD=∠MAC+∠BAM=90°,
∴∠MCD=90°,
在Rt△NCD中,CN=3,CD=1,
根据勾股定理得,ND= ![]() ,
,
∵∠MAD=90°,∠MAN=45°,
∴∠DAN=45°,
∵AM=AD,AN=AN,
∴△MAN≌△DAN,
∴MN=DN= ![]() ,
,
所以答案是 ![]() .
.
【考点精析】认真审题,首先需要了解全等三角形的性质(全等三角形的对应边相等; 全等三角形的对应角相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,(M2,N2),∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.
(1)求证:△ADE≌△CDB;
(2)若BC=
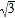 ,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【阅读理解】
我们知道,当a>0且b>0时,( ﹣
﹣ 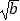 )2≥0,所以a﹣2
)2≥0,所以a﹣2 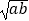 +≥0,从而a+b≥2
+≥0,从而a+b≥2 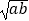 (当a=b时取等号),
(当a=b时取等号),
【获得结论】设函数y=x+ (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x=  即x=
即x=  时,函数y有最小值为2
时,函数y有最小值为2 
(1)【直接应用】
若y1=x(x>0)与y2=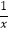 (x>0),则当x=时,y1+y2取得最小值为 .
(x>0),则当x=时,y1+y2取得最小值为 .
(2)【变形应用】
若y1=x+1(x>﹣1)与y2=(x+1)2+4(x>﹣1),则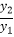 的最小值是
的最小值是
(3)【探索应用】
在平面直角坐标系中,点A(﹣3,0),点B(0,﹣2),点P是函数y=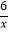 在第一象限内图象上的一个动点,过P点作PC⊥x轴于点C,PD⊥y轴于点D,设点P的横坐标为x,四边形ABCD的面积为S
在第一象限内图象上的一个动点,过P点作PC⊥x轴于点C,PD⊥y轴于点D,设点P的横坐标为x,四边形ABCD的面积为S
①求S与x之间的函数关系式;
②求S的最小值,判断取得最小值时的四边形ABCD的形状,并说明理由.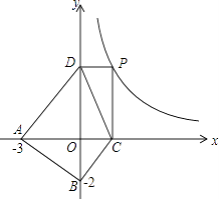
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,为厉行节能减排,倡导绿色出行,某公司拟在我市甲、乙两个街道社区投放一批共享单车(俗称“小黄车”),这批自行车包括A、B两种不同款型.
成本单价 (单位:元)
投放数量
(单位:辆)
总价(单位:元)
A型
x
50
50x
B型
x+10
50
成本合计(单位:元)
7500
问题1:看表填空
如图2所示,本次试点投放的A、B型“小黄车”共有 辆;用含有x的式子表示出B型自行车的成本总价为 ;
问题2:自行车单价
试求A、B两型自行车的单价各是多少?
问题3:投放数量
现在该公司采取如下方式投放A型“小黄车”:甲街区每100人投放n辆,乙街区每100人投放(n+2)辆,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有
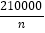 人,求甲街区每100人投放A型“小黄车”的数量.
人,求甲街区每100人投放A型“小黄车”的数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
(1)求抛物线的解析式;
(2)如图1,过点P作BD的平行线,交AB于点Q,连接DQ,设AQ=m,△PDQ的面积为S,求S关于m的函数解析式,以及S的最大值;
(3)如图2,抛物线对称轴与x轴交与点G,E为OG的中点,F为点C关于DG对称的对称点,过点P分别作直线EF、DG的垂线,垂足为M、N,连接MN,直接写出△PMN为等腰三角形时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形
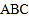 中,
中, ,求
,求 的度数.(答案:
的度数.(答案: )
)例2 等腰三角形
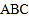 中,
中, ,求
,求 的度数.(答案:
的度数.(答案: 或
或 或
或 )
)张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形
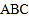 中,
中, ,求
,求 的度数.
的度数.(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,
 的度数不同,得到
的度数不同,得到 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形 中,设
中,设 ,当
,当 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索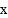 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)运用完全平方公式计算:992
(2)先化简,再求值:(2x+3y)2﹣(2x+y)(2x﹣y),其中 x=
 ,y=
,y= .
.
相关试题

