【题目】【阅读理解】
我们知道,当a>0且b>0时,( ![]() ﹣
﹣ ![]() )2≥0,所以a﹣2
)2≥0,所以a﹣2 ![]() +≥0,从而a+b≥2
+≥0,从而a+b≥2 ![]() (当a=b时取等号),
(当a=b时取等号),
【获得结论】设函数y=x+ ![]() (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x= ![]() 即x=
即x= ![]() 时,函数y有最小值为2
时,函数y有最小值为2 ![]()
(1)【直接应用】
若y1=x(x>0)与y2= ![]() (x>0),则当x=时,y1+y2取得最小值为 .
(x>0),则当x=时,y1+y2取得最小值为 .
(2)【变形应用】
若y1=x+1(x>﹣1)与y2=(x+1)2+4(x>﹣1),则 ![]() 的最小值是
的最小值是
(3)【探索应用】
在平面直角坐标系中,点A(﹣3,0),点B(0,﹣2),点P是函数y= ![]() 在第一象限内图象上的一个动点,过P点作PC⊥x轴于点C,PD⊥y轴于点D,设点P的横坐标为x,四边形ABCD的面积为S
在第一象限内图象上的一个动点,过P点作PC⊥x轴于点C,PD⊥y轴于点D,设点P的横坐标为x,四边形ABCD的面积为S
①求S与x之间的函数关系式;
②求S的最小值,判断取得最小值时的四边形ABCD的形状,并说明理由.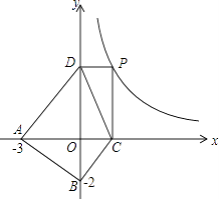
参考答案:
【答案】
(1)1;2
(2)4
(3)
解:①设P(x, ![]() ),则C(x,0),D(0,
),则C(x,0),D(0, ![]() ),
),
∴AC=x+3,BD= ![]() +2,
+2,
∴S= ![]() ACBD=
ACBD= ![]() (x+3)(
(x+3)( ![]() +2)=6+x+
+2)=6+x+ ![]() ;
;
②∵x>0,
∴x+ ![]() ≥2
≥2 ![]() =6,
=6,
∴当x= ![]() 时,即x=3时,x+
时,即x=3时,x+ ![]() 有最小值6,
有最小值6,
∴此时S=6+x+ ![]() 有最小值12,
有最小值12,
∵x=3,
∴P(3,2),C(3,0),D(0,2),
∴A、C关于x轴对称,D、B关于y轴对称,即四边形ABCD的对角线互相垂直平分,
∴四边形ABCD为菱形.
【解析】解:(1)∵x>0,∴y1+y2=x+ ![]() ≥2
≥2 ![]() =2,∴当x=
=2,∴当x= ![]() 时,即x=1时,y1+y2有最小值2,所以答案是:1;2;(2)∵x>﹣1,∴x+1>0,∴
时,即x=1时,y1+y2有最小值2,所以答案是:1;2;(2)∵x>﹣1,∴x+1>0,∴ ![]() =
= ![]() =(x+1)+
=(x+1)+ ![]() ≥2
≥2 ![]() =4,∴当x+1=
=4,∴当x+1= ![]() 时,即x=1时,
时,即x=1时, ![]() 有最小值4,所以答案是:4;
有最小值4,所以答案是:4;
【考点精析】本题主要考查了反比例函数的性质的相关知识点,需要掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能正确解答此题.
-
科目: 来源: 题型:
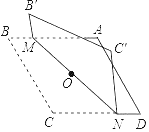
查看答案和解析>>【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现要把192吨物资从我市运往甲、乙两地,用大、小两种货车共18辆恰好能一次性运完这批物资.已知这两种货车的载重量分别为14吨/辆和8吨/辆,运往甲、乙两地的运费如表:
运往地
车型甲地(元/辆)
乙地(元/辆)
大货车
720
800
小货车
500
650
(1)求这两种货车各用多少辆?
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式;
(3)在(2)的条件下,若运往甲地的物资部少于96吨,请你设计出使总运费最低的货车调配方案,并求出最少总运费. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,(M2,N2),∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.
(1)求证:△ADE≌△CDB;
(2)若BC=
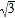 ,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.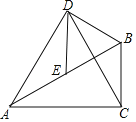
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,为厉行节能减排,倡导绿色出行,某公司拟在我市甲、乙两个街道社区投放一批共享单车(俗称“小黄车”),这批自行车包括A、B两种不同款型.
成本单价 (单位:元)
投放数量
(单位:辆)
总价(单位:元)
A型
x
50
50x
B型
x+10
50
成本合计(单位:元)
7500
问题1:看表填空
如图2所示,本次试点投放的A、B型“小黄车”共有 辆;用含有x的式子表示出B型自行车的成本总价为 ;
问题2:自行车单价
试求A、B两型自行车的单价各是多少?
问题3:投放数量
现在该公司采取如下方式投放A型“小黄车”:甲街区每100人投放n辆,乙街区每100人投放(n+2)辆,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有
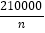 人,求甲街区每100人投放A型“小黄车”的数量.
人,求甲街区每100人投放A型“小黄车”的数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:
如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC、CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.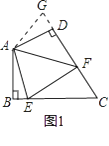
(1)小明同学探究此问题的方法是,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;
(2)探索延伸:
如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF= ∠BAD,上述结论是否仍然成立,请说明理由;
∠BAD,上述结论是否仍然成立,请说明理由; 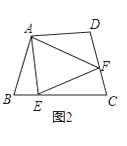
(3)实际应用:
如图③,在某次军事演习中,舰艇甲在指挥中心O北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,当∠EOF=70°时,两舰艇之间的距离是海里.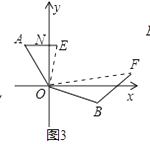
(4)能力提高:
如图④,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为 .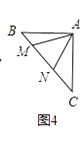
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
(1)求抛物线的解析式;
(2)如图1,过点P作BD的平行线,交AB于点Q,连接DQ,设AQ=m,△PDQ的面积为S,求S关于m的函数解析式,以及S的最大值;
(3)如图2,抛物线对称轴与x轴交与点G,E为OG的中点,F为点C关于DG对称的对称点,过点P分别作直线EF、DG的垂线,垂足为M、N,连接MN,直接写出△PMN为等腰三角形时点P的坐标.
相关试题

