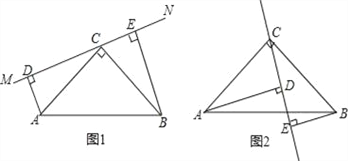
【题目】如图(1)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.求证:
(1)△ADC≌△CEB;
(2)DE=AD+BE.
(3)当直线MN绕点C旋转到图(2)的位置时,DE、AD、BE又怎样的关系?并加以证明.
参考答案:
【答案】证明见解析.
【解析】试题分析:(1)由AAS可证明△ADC≌△CEB;
(2)再利用线段的和差可证得结论;
(3)同(2)的方法可证得结论.
试题解析:(1)证明:∵∠ACB=90°,∴∠ACD+∠BCE=90°,而AD⊥MN于D,BE⊥MN于E,∴∠ADC=∠CEB=90°,∠BCE+∠CBE=90°,∴∠ACD=∠CBE.
在△ADC和△CEB中,∵∠ADC=∠CEB,∠ACD=∠CBE,AC=BC,∴△ADC≌△CEB(AAS);
(2)∵△ADC≌△CEB,∴AD=CE,DC=BE,∴DE=DC+CE=BE+AD;
(3)解:DE=AD﹣BE.理由如下:
在△ADC和△CEB中,∵∠ADC=∠CEB,∠ACD=∠CBE,AC=BC,∴△ADC≌△CEB(AAS),∴AD=CE,DC=BE,∴DE=CE﹣CD=AD﹣BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长和宽分别是a、b的长方形纸片的四个角都剪去一个边长为x的正方形,折叠后,做成一无盖的盒子(单位:cm)

(1)用a,b,x表示纸片剩余部分的面积;
(2)用a,b,x表示盒子的体积;
(3)当a=10,b=8且剪去的每一个小正方形的面积等于4cm2时,求剪去的每一个小正方形的边长及所做成盒子的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD的对角线AC,BD相交于直角坐标系的原点O,点A,B的坐标分别为(-1,3),(1,2).则点C的坐标成为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=60°,∠B=50°, BC边上的垂直平分线DE交BC、AB分别于点D、E,△AEC的周长是13,BC=6。求∠ACE的度数和△ABC的周长。

-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形有两条边的长为4cm和9cm,则该三角形的周长( )
A. 17cm B. 22cm C. 17cm和22cm D. 18cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】购买一本书,打八折比打九折少花2元钱,那么这本书的原价是 元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,AB=AC,D,E是斜边上BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
①BF⊥BC;②△AED≌△AEF;③BE+DC=DE;④BE2+DC2=DE2
其中正确的个数是( )
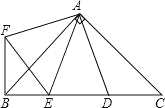
A.1 B.2 C.3 D.4
相关试题

