【题目】已知函数y=x2﹣(m﹣2)x+m的图象过点(﹣1,15),设其图象与x轴交于点A,B(A在B的左侧),点C在图象上,且S△ABC=1,求:
(1)求m;
(2)求点A,点B的坐标;
(3)求点C的坐标.
参考答案:
【答案】
(1)解:∵函数y=x2﹣(m﹣2)x+m的图象过点(﹣1,15),
∴15=1+m﹣2+m,
解得:m=8
(2)解:将m=8代入y=x2﹣(m﹣2)x+m中得:y=x2﹣6x+8,
令y=0,则x2﹣6x+8=0,
解得:x1=2,x2=4,
∵A在B的左侧,
∴点A的坐标为(2,0),点B的坐标为(4,0)
(3)解:设点C的坐标为(n,n2﹣6n+8),
∵A(2,0),B(4,0),
∴AB=2,
S△ABC= ![]() AB|n2﹣6n+8|=1=|n2﹣6n+8|,
AB|n2﹣6n+8|=1=|n2﹣6n+8|,
解得:n1=1,n2=6,n3=3,
∴点C的坐标为(1,1)、(6,1)或(3,﹣1)
【解析】(1)将点(﹣1,15)代入y=x2﹣(m﹣2)x+m中可得出关于m的一元一次方程,解方程即可得出结论;(2)将m得值代入函数解析式中,令y=0可得出关于x的一元二次方程,解方程即可得出点A、B的坐标;(3)设点C的坐标为(n,n2﹣6n+8),根据点A、B的坐标结合S△ABC=1,即可得出关于n的含绝对值的一元二次方程,解方程即可得出n的值,进而可得出点C的坐标.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a+2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2 .
上述4个判断中,正确的是( )
A.①②
B.①②④
C.①③④
D.②③④ -
科目: 来源: 题型:
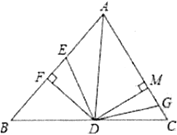
查看答案和解析>>【题目】如图,在△ABC中,∠BAD=∠DAC,DF上AB,DM⊥AC,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.当t=________秒时,△DFE与△DMG全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣
 x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C,D同时出发,当动点D到达原点O时,点C,D停止运动.
x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C,D同时出发,当动点D到达原点O时,点C,D停止运动.
(1)直接写出抛物线的解析式:;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB.

(1)求点P与点P′之间的距离;
(2)求∠APB的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程x2+2(m﹣2)x+m2+4=0有两个实数根,且两个根的平方和比两根的积大40,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据条件求二次函数的解析式
(1)二次函数y=ax2+bx+c的对称轴为x=3,最小值为﹣2,且过(0,1)点.
(2)抛物线过(﹣1,0),(3,0),(1,﹣5)三点.
相关试题

