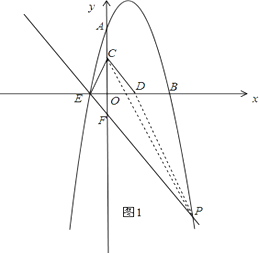
【题目】如图,已知抛物线y=﹣ ![]() x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C,D同时出发,当动点D到达原点O时,点C,D停止运动.
x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C,D同时出发,当动点D到达原点O时,点C,D停止运动.
(1)直接写出抛物线的解析式:;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)y=﹣ ![]() x2+3x+8
x2+3x+8
(2)
解:∵点A(0,8)、B(8,0),
∴OA=8,OB=8,
令y=0,得:﹣ ![]() x2+3x+8=0,
x2+3x+8=0,
解得:x1=8,x2=﹣2,
∵点E在x轴的负半轴上,
∴点E(﹣2,0),
∴OE=2,
根据题意得:当D点运动t秒时,BD=t,OC=t,
∴OD=8﹣t,
∴DE=OE+OD=10﹣t,
∴S= ![]() DEOC=
DEOC= ![]() (10﹣t)t=﹣
(10﹣t)t=﹣ ![]() t2+5t,
t2+5t,
即S=﹣ ![]() t2+5t=﹣
t2+5t=﹣ ![]() (t﹣5)2+
(t﹣5)2+ ![]() ,
,
∴当t=5时,S最大= ![]()
(3)
解:方法一:
由(2)知:当t=5时,S最大= ![]() ,
,
∴当t=5时,OC=5,OD=3,
∴C(0,5),D(3,0),
由勾股定理得:CD= ![]() ,
,
设直线CD的解析式为:y=kx+b,
将C(0,5),D(3,0),代入上式得:
k=﹣ ![]() ,b=5,
,b=5,
∴直线CD的解析式为:y=﹣ ![]() x+5,
x+5,
过E点作EF∥CD,交抛物线与点P,如图1,
设直线EF的解析式为:y=﹣ ![]() x+b,
x+b,
将E(﹣2,0)代入得:b=﹣ ![]() ,
,
∴直线EF的解析式为:y=﹣ ![]() x﹣
x﹣ ![]() ,
,
将y=﹣ ![]() x﹣
x﹣ ![]() ,与y=﹣
,与y=﹣ ![]() x2+3x+8联立成方程组得:
x2+3x+8联立成方程组得:
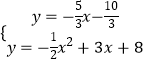 ,
,
解得: ![]() ,
, 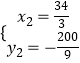 ,
,
∴P( ![]() ,﹣
,﹣ ![]() );
);
过点E作EG⊥CD,垂足为G,
∵当t=5时,S△ECD= ![]() =
= ![]() ,
,
∴EG= ![]() ,
,
过点D作DN⊥CD,垂足为N,且使DN= ![]() ,过点N作NM⊥x轴,垂足为M,如图2,
,过点N作NM⊥x轴,垂足为M,如图2,
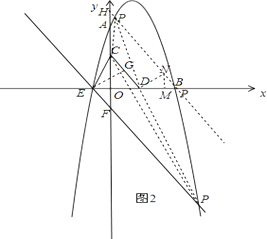
可得△EGD∽△DMN,
∴ ![]() ,
,
即:  ,
,
解得:DM= ![]() ,
,
∴OM= ![]() ,
,
由勾股定理得:MN= ![]() =
= ![]() ,
,
∴N( ![]() ,
, ![]() ),
),
过点N作NH∥CD,与抛物线交与点P,如图2,
设直线NH的解析式为:y=﹣ ![]() x+b,
x+b,
将N( ![]() ,
, ![]() ),代入上式得:b=
),代入上式得:b= ![]() ,
,
∴直线NH的解析式为:y=﹣ ![]() x+
x+ ![]() ,
,
将y=﹣ ![]() x+
x+ ![]() ,与y=﹣
,与y=﹣ ![]() x2+3x+8联立成方程组得:
x2+3x+8联立成方程组得:
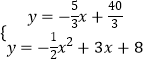 ,
,
解得: ![]() ,
, 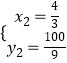 ,
,
∴P(8,0)或P( ![]() ,
, ![]() ),
),
综上所述:当△CED的面积最大时,在抛物线上存在点P(点E除外),使△PCD的面积等于△CED的最大面积,点P的坐标为:P( ![]() ,﹣
,﹣ ![]() )或P(8,0)或P(
)或P(8,0)或P( ![]() ,
, ![]() ).
).
方法二:
由(2)知,C(0,5),D(3,0),∴lCD:y=﹣ ![]() x+5,
x+5,
作PH⊥x轴,交CD于点H,
∵P在抛物线上,∴设P(6m,﹣18m2+18m+8),
∴H(6m,﹣10m+5),C(0,5),D(3,0),
S△PCD= ![]() |(DX﹣CX)(PY﹣HY)|,
|(DX﹣CX)(PY﹣HY)|,
∵S△CED= ![]() ,
,
∴ ![]() ,
,
∴3×|18m2﹣28m﹣3|=25,
①3×(18m2﹣28m﹣3)=25,
∴m1=﹣ ![]() ,m2=
,m2= ![]() ,
,
∴6m1=﹣2(舍),6m2= ![]() ,
,
②3×(18m2﹣28m﹣3)=﹣25,
∴m1= ![]() ,m2=
,m2= ![]() ,
,
∴6m1=8,6m2= ![]() ,
,
综上所述,点P的坐标为:P( ![]() ,﹣
,﹣ ![]() )或P(8,0)或P(
)或P(8,0)或P( ![]() ,
, ![]() )
)
【解析】解:(1)将点A(0,8)、B(8,0)代入抛物线y=﹣ ![]() x2+bx+c得:
x2+bx+c得: 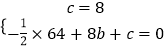 ,
,
解得:b=3,c=8,
∴抛物线的解析式为:y=﹣ ![]() x2+3x+8,
x2+3x+8,
所以答案是:y=﹣ ![]() x2+3x+8;
x2+3x+8;
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是( )
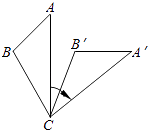
A.110°
B.80°
C.40°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a+2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2 .
上述4个判断中,正确的是( )
A.①②
B.①②④
C.①③④
D.②③④ -
科目: 来源: 题型:
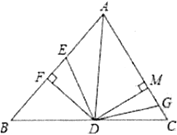
查看答案和解析>>【题目】如图,在△ABC中,∠BAD=∠DAC,DF上AB,DM⊥AC,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.当t=________秒时,△DFE与△DMG全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=x2﹣(m﹣2)x+m的图象过点(﹣1,15),设其图象与x轴交于点A,B(A在B的左侧),点C在图象上,且S△ABC=1,求:
(1)求m;
(2)求点A,点B的坐标;
(3)求点C的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB.

(1)求点P与点P′之间的距离;
(2)求∠APB的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程x2+2(m﹣2)x+m2+4=0有两个实数根,且两个根的平方和比两根的积大40,求m的值.
相关试题

