【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a+2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2 .
上述4个判断中,正确的是( )
A.①②
B.①②④
C.①③④
D.②③④
参考答案:
【答案】B
【解析】解:∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
∴b2>4ac,故①正确,
由图象可知,x=2时,y<0,
∴4a=2b+c<0,故②正确,
由图象可知,不等式ax2+bx+c>0的解集是x<x1或x>x2(x1 , x2分别抛物线与x轴解得的横坐标,x1是左交点横坐标),故③错误,
由图象可知,点(5,y2)分、到对称轴的距离比点(﹣2,y1)到对称轴的距离大,
∴y2>y1 , 故④正确.
故选B.
【考点精析】关于本题考查的二次函数图象以及系数a、b、c的关系,需要了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形纸片△ABC,AB=8,BC=6,AC=5,沿过点B的直线折叠这个三角形,折痕为BD(点D在线段AC上且不与A、C重合).若点C落在AB边下方的点E处,则△ADE的周长p的取值范围是( )

A. 7<p<10 B. 5<p<10 C. 5<p<7 D. 7<p<19
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
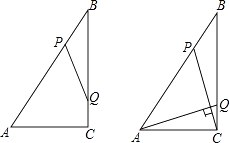
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ,CP,若AQ⊥CP,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是( )
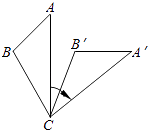
A.110°
B.80°
C.40°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAD=∠DAC,DF上AB,DM⊥AC,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.当t=________秒时,△DFE与△DMG全等.
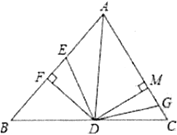
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣
 x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C,D同时出发,当动点D到达原点O时,点C,D停止运动.
x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C,D同时出发,当动点D到达原点O时,点C,D停止运动.
(1)直接写出抛物线的解析式:;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=x2﹣(m﹣2)x+m的图象过点(﹣1,15),设其图象与x轴交于点A,B(A在B的左侧),点C在图象上,且S△ABC=1,求:
(1)求m;
(2)求点A,点B的坐标;
(3)求点C的坐标.
相关试题

