搜索
【题目】如图，Rt△ABC，∠C=90°，CA=CB=4
cm，点P为AB边上的一个动点，点E是CA边的中点, 连接PE，设A，P两点间的距离为xcm，P，E两点间的距离为y cm.小安根据学习函数的经验，对函数
随自变量
的变化而变化的规律进行了探究．
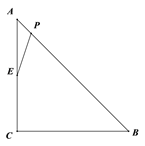
下面是小安的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了与的几组值，如下表：
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y/cm | 2.8 | 2.2 | 2.0 | 2.2 | 2.8 | 3.6 | 5.4 | 6.3 |
（说明：补全表格时相关数值保留一位小数）
（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：
①写出该函数的一条性质： ；
②当
时，
的长度约为 cm.
参考答案：
【答案】（1）4.5;（2）见解析；（3）1.1cm
【解析】试题分析：
如图所示：过点
作
于点
根据勾股定理求解即可.
秒点，连线即可.
根据图象回答即可.
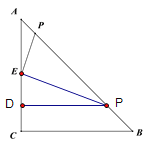
试题解析：如图所示：过点作于点
易求
故答案为：4.5.
（2）如图：
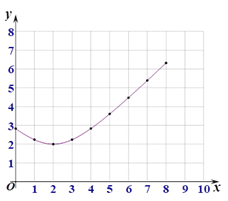
（3）①该函数有最小值或最大值；或当x＞2时，y随x的增大而增大.
②当
时，
的长度约为1.1cm.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在平面直角坐标系中,以A(3,0)为圆心,以5为半径的圆与x轴相交于B. C,与y轴的负半轴相交于D,抛物线y=x
+bx+c经过B. C. D三点。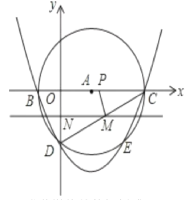
(1)求此抛物线的解析式；
(2)若动直线MN(MN∥x轴)从点D开始，以每秒1个长度单位的速度沿y轴的正方向移动，且与线段CD、y轴分别交于M、N两点，动点P同时从点C出发，在线段OC上以每秒2个长度单位的速度向原点O运动，连接PM，设运动时间为t秒，若以P、C. M为顶点的三角形与△OCD相似，求实数t的值；
②当t为何值时,
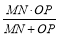的值最大，并求出最大值。 -
科目： 来源： 题型：
查看答案和解析>>【题目】某商场服装部为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励．为了确定一个适当的月销售目标，商场服装部统计了每个营业员在某月的销售额（单位：万元），数据如下，请补充完整．
收集数据 17 18 16 12 24 15 27 25 18 19
22 17 16 19 31 29 16 14 15 25
15 31 23 17 15 15 27 27 16 19
整理、描述数据
销售额/万元
12
14
15
16
17
18
19
22
23
24
25
27
29
31
人数
1
1
4
3
2
1
1
1
2
3
1
2
分析数据 样本数据的平均数、众数、中位数如下表所示：
平均数
众数
中位数
20
18
得出结论 ⑴如果想让一半左右的营业员都能达到销售目标，你认为月销售额应定为 万元．
⑵如果想确定一个较高的销售目标，这个目标可以定为每月 万元，理由为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在4×4的正方形网格中，△ABC的顶点都在格点上，下列结论错误的是（ ）
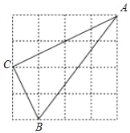
A. AB＝5 B. ∠C＝90° C. AC＝2
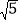D. ∠A＝30° -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知Rt△ABC中，∠C=90°，∠BAC=30°，点D为边BC上的点，连接AD，∠BAD=α，点D关于AB的对称点为E，点E关于AC的对称点为G，线段EG交AB于点F，连接AE，DE，DG，AG.
（1）依题意补全图形；
（2）求∠AGE的度数（用含α的式子表示）；
（3）用等式表示线段EG与EF，AF之间的数量关系，并说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=5，AC=13，BC边上的中线AD=6，则△ABD的面积是______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，当图形W上的点P的横坐标和纵坐标相等时，则称点P为图形W的“梦之点”.
（1）已知⊙O的半径为1.
①在点E（1,1），F（
,－
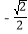）,M(－2，－2)中，⊙O的“梦之点”为 ；②若点P位于⊙O内部，且为双曲线
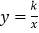（k≠0）的“梦之点”，求k的取值范围.（2）已知点C的坐标为（1，t），⊙C的半径为
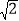，若在⊙C上存在“梦之点”P，直接写出t的取值范围.（3）若二次函数
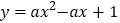的图象上存在两个“梦之点”
，
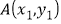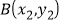,且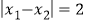
，求二次函数图象的顶点坐标.
相关试题
