【题目】如图,在平面直角坐标系中,以A(3,0)为圆心,以5为半径的圆与x轴相交于B. C,与y轴的负半轴相交于D,抛物线y=x![]() +bx+c经过B. C. D三点。
+bx+c经过B. C. D三点。
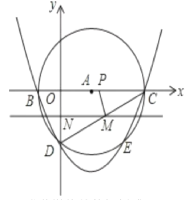
(1)求此抛物线的解析式;
(2)若动直线MN(MN∥x轴)从点D开始,以每秒1个长度单位的速度沿y轴的正方向移动,且与线段CD、y轴分别交于M、N两点,动点P同时从点C出发,在线段OC上以每秒2个长度单位的速度向原点O运动,连接PM,设运动时间为t秒,若以P、C. M为顶点的三角形与△OCD相似,求实数t的值;
②当t为何值时,![]() 的值最大,并求出最大值。
的值最大,并求出最大值。
参考答案:
【答案】(1)y=![]() x
x![]()
![]() x4;(2)t=2或t=
x4;(2)t=2或t=![]() ,②当t=2时取最大值2;
,②当t=2时取最大值2;
【解析】
(1)直接利用圆的性质得出B,C点坐标,进而利用交点式求出函数解析式;
(2)①直接利用若△PCM∽△OCD或△MCP∽△OCD,分别得出t的值求出答案即可;
②利用MN∥OC,则![]() ,进而求出
,进而求出![]() 关于t的关系式求出最值即可.
关于t的关系式求出最值即可.
(1)∵A(3,0)为圆心,以5为半径的圆与x轴相交于B. C,
∴B(2,0),C(8,0),
代入抛物线y=![]() (x+2)(x8),
(x+2)(x8),
得y=![]() x
x![]()
![]() x4;
x4;
(2)①由题可得N(0,t4),P(82t,0),
若△PCM∽△OCD,
则![]() ,即
,即![]() ,
,
解得t=2;
若△MCP∽△OCD,则![]() ,即
,即![]() ,
,
解得t=![]() ,
,
即当t=2或t=![]() 时,以P、C. M为顶点的三角形与△OCD相似。
时,以P、C. M为顶点的三角形与△OCD相似。
②∵MN∥OC,
![]() ,即MN=2t,
,即MN=2t,
又∵OP=82t,
∴![]() ,
,
∴当t=2时取最大值2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,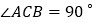 ,点
,点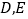 分别是
分别是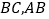 上的中点,连接
上的中点,连接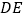 并延长至点
并延长至点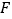 ,使
,使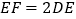 ,连接
,连接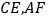 .
.(1)证明:
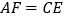 ;
;(2)若
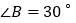 ,AC=2,连接BF,求BF的长
,AC=2,连接BF,求BF的长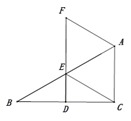
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:(ⅰ)如果两个函数
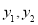 ,存在
,存在 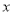 取同一个值,使得
取同一个值,使得 ,那么称
,那么称 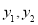 为“互联互通函数”,称对应的
为“互联互通函数”,称对应的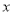 值为
值为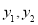 的“互联点”; (ⅱ)如果两个函数
的“互联点”; (ⅱ)如果两个函数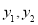 为“互联互通函数”,那么
为“互联互通函数”,那么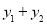 的最大值称为
的最大值称为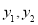 的“互通值”.
的“互通值”.(1)判断函数
 与
与 是否为“互通互联函数”,如果是,请求出
是否为“互通互联函数”,如果是,请求出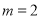 时他们的“互联点”,如果不是,请说明理由;
时他们的“互联点”,如果不是,请说明理由;(2)当
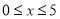 时,已知函数
时,已知函数 与
与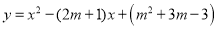 是“互联互通函数”.且有唯一“互联点”;
是“互联互通函数”.且有唯一“互联点”;①求出
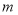 的取值范围;
的取值范围;②若他们的“互通值”为18 ,试求出
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、BF分别是⊙O的直径和弦,弦CD与AB、BF分别相交于点E、G,过点F的切线HF与DC的延长线相交于点H,且HF=HG.
(1)求证:AB⊥CD;
(2)若sin∠HGF=
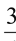 ,BF=3,求⊙O的半径长.
,BF=3,求⊙O的半径长.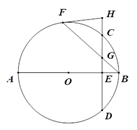
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元),数据如下,请补充完整.
收集数据 17 18 16 12 24 15 27 25 18 19
22 17 16 19 31 29 16 14 15 25
15 31 23 17 15 15 27 27 16 19
整理、描述数据
销售额/万元
12
14
15
16
17
18
19
22
23
24
25
27
29
31
人数
1
1
4
3
2
1
1
1
2
3
1
2
分析数据 样本数据的平均数、众数、中位数如下表所示:
平均数
众数
中位数
20
18
得出结论 ⑴如果想让一半左右的营业员都能达到销售目标,你认为月销售额应定为 万元.
⑵如果想确定一个较高的销售目标,这个目标可以定为每月 万元,理由为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在4×4的正方形网格中,△ABC的顶点都在格点上,下列结论错误的是( )
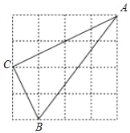
A. AB=5 B. ∠C=90° C. AC=2
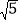 D. ∠A=30°
D. ∠A=30° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC,∠C=90°,CA=CB=4
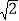 cm,点P为AB边上的一个动点,点E是CA边的中点, 连接PE,设A,P两点间的距离为xcm,P,E两点间的距离为y cm.小安根据学习函数的经验,对函数
cm,点P为AB边上的一个动点,点E是CA边的中点, 连接PE,设A,P两点间的距离为xcm,P,E两点间的距离为y cm.小安根据学习函数的经验,对函数 随自变量
随自变量 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.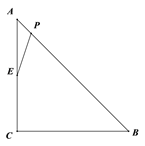
下面是小安的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了
 与
与 的几组值,如下表:
的几组值,如下表:x/cm
0
1
2
3
4
5
6
7
8
y/cm
2.8
2.2
2.0
2.2
2.8
3.6
5.4
6.3
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:
①写出该函数的一条性质: ;
②当
 时,
时,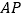 的长度约为 cm.
的长度约为 cm.
相关试题

