【题目】在平面直角坐标系xOy中,当图形W上的点P的横坐标和纵坐标相等时,则称点P为图形W的“梦之点”.
(1)已知⊙O的半径为1.
①在点E(1,1),F(![]() ,-
,-![]() ),M(-2,-2)中,⊙O的“梦之点”为 ;
),M(-2,-2)中,⊙O的“梦之点”为 ;
②若点P位于⊙O内部,且为双曲线![]() (k≠0)的“梦之点”,求k的取值范围.
(k≠0)的“梦之点”,求k的取值范围.
(2)已知点C的坐标为(1,t),⊙C的半径为![]() ,若在⊙C上存在“梦之点”P,直接写出t的取值范围.
,若在⊙C上存在“梦之点”P,直接写出t的取值范围.
(3)若二次函数![]() 的图象上存在两个“梦之点”
的图象上存在两个“梦之点”![]() ,
,![]() ,且
,且![]() ,求二次函数图象的顶点坐标.
,求二次函数图象的顶点坐标.
参考答案:
【答案】(1)①F; ②![]() (2)-1≤t≤3 ;(3)坐标为(
(2)-1≤t≤3 ;(3)坐标为(![]() ),(
),(![]() )
)
【解析】试题分析:![]() ①根据 “梦之点”的概念直接判断即可.
①根据 “梦之点”的概念直接判断即可.
②先求出⊙O的“梦之点”坐标为![]() 和
和![]() .将
.将![]() 代入双曲线表达式中,得,
代入双曲线表达式中,得,![]() 即可求出k的取值范围.
即可求出k的取值范围.
![]() ⊙C 要和直线y=x的交点均为双曲线的“梦之点”, 在⊙C上存在“梦之点”P,即它们的必须有交点.
⊙C 要和直线y=x的交点均为双曲线的“梦之点”, 在⊙C上存在“梦之点”P,即它们的必须有交点.
![]() 由“梦之点”定义可得:
由“梦之点”定义可得: ![]() ,
,![]() .则
.则![]() .
.
整理得,![]() ,解得,
,解得,![]() ,
,![]() . 把两个根代入
. 把两个根代入![]() 中,求出
中,求出![]() 的值,分别计算即可.
的值,分别计算即可.
试题解析:(1)①F;
②∵⊙O的半径为1.
∴⊙O的“梦之点”坐标为![]() 和
和![]() .
.
又∵双曲线![]() (k≠0)与直线y=x的交点均为圆的“梦之点”,
(k≠0)与直线y=x的交点均为圆的“梦之点”,
∴将![]() 代入双曲线表达式中,得,
代入双曲线表达式中,得,![]()
∵点P位于⊙O内部.
∴![]() ,
,
(2)-1≤t≤3,
(3)由“梦之点”定义可得: ![]() ,
,![]() .
.
则![]() .
.
整理得,![]() ,
,
解得,![]() ,
,![]() .
.
把两个根代入![]() 中,即
中,即![]() ,
,
解得,![]() ,
,![]() .
.
当![]() 时,
时,![]() ,其顶点坐标为
,其顶点坐标为![]()
当![]() 时,
时,![]() ,其顶点坐标为
,其顶点坐标为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC,∠C=90°,CA=CB=4
 cm,点P为AB边上的一个动点,点E是CA边的中点, 连接PE,设A,P两点间的距离为xcm,P,E两点间的距离为y cm.小安根据学习函数的经验,对函数
cm,点P为AB边上的一个动点,点E是CA边的中点, 连接PE,设A,P两点间的距离为xcm,P,E两点间的距离为y cm.小安根据学习函数的经验,对函数 随自变量
随自变量 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.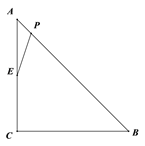
下面是小安的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了
 与
与 的几组值,如下表:
的几组值,如下表:x/cm
0
1
2
3
4
5
6
7
8
y/cm
2.8
2.2
2.0
2.2
2.8
3.6
5.4
6.3
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:
①写出该函数的一条性质: ;
②当
 时,
时,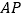 的长度约为 cm.
的长度约为 cm. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠C=90°,∠BAC=30°,点D为边BC上的点,连接AD,∠BAD=α,点D关于AB的对称点为E,点E关于AC的对称点为G,线段EG交AB于点F,连接AE,DE,DG,AG.
(1)依题意补全图形;
(2)求∠AGE的度数(用含α的式子表示);
(3)用等式表示线段EG与EF,AF之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6,则△ABD的面积是______.

-
科目: 来源: 题型:
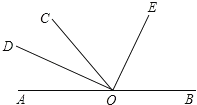
查看答案和解析>>【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)写出图中小于平角的角.
(2)求出∠BOD的度数.
(3)小明发现OE平分∠BOC,请你通过计算说明道理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富学生的课外活动,某校决定购买100个篮球和a(a>10)副羽毛球拍.经调查发现:甲、乙两个体育用品商店以同样的价格出售同种品牌的篮球和羽毛球拍.已知每个篮球比每副羽毛球拍贵25元,两个篮球与三副羽毛球拍的费用正好相等.经洽谈,甲商店的优惠方案是:每购买十个篮球,送一副羽毛球拍;乙商店的优惠方案是:若购买篮球数超过80个,则购买羽毛球拍可打八折.
(1)设每个篮球x元,则每副羽毛球拍______元(用含x的代数表示);并求出每个篮球和每副羽毛球拍的价格分别是多少?
(2)请用含a的代数式分别表示出到甲商店和乙商店购买所花的费用;
(3)请你决策:在哪一家商店购买划算?(直接写出结论)
-
科目: 来源: 题型:
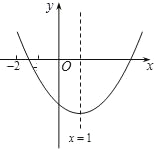
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论:
(1)c<0;
(2)b>0;
(3)4a+2b+c>0;
(4)(a+c)2<b2.
其中不正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

