【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
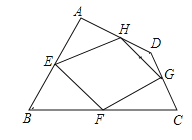
(1)四边形EFGH的形状是 ,证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? .
参考答案:
【答案】(1)平行四边形,证明见解析.
(2)四边形ABCD的对角线满足互相垂直,证明见解析,
(3)菱形,证明见解析.
【解析】
(1)连接BD,根据三角形的中位线定理得到EH∥BD,EH=![]() BD,FG∥BD,FG═
BD,FG∥BD,FG═![]() BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
(2)根据有一个角是直角的平行四边形是矩形,可知当四边形ABCD的对角线满足AC⊥BD的条件时,四边形EFGH是矩形;
(3)菱形的中点四边形是矩形.根据三角形的中位线平行于第三边并且等于第三边的一半可得四边形EFGH是平行四边形,再根据矩形的每一个角都是直角,然后根据平行线的性质,再根据垂直定义解答;
解:(1)四边形EFGH的形状是平行四边形.理由如下:
如图,连结BD. ∵E、H分别是AB、AD中点,
∴EH∥BD,EH= ![]() BD,
BD,
同理FG∥BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
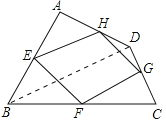
故答案为:平行四边形.
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.
理由如下: 如图,连结AC、BD.
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD, ∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形;
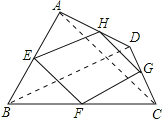
故答案为:对角线互相垂直.
(3)菱形的中点四边形是矩形.
理由如下: 如图,连结AC、BD. ∵E、F、G、H分别为四边形ABCD四条边上的中点, ∴EH∥BD,HG∥AC,FG∥BD,EH=![]() BD,FG=
BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,
∵EH∥BD,HG∥AC,
∴EH⊥HG,
∴平行四边形EFGH是矩形;
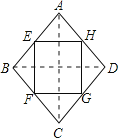
故答案为:菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的个数是 ( )
①若三条线段的比为1:1:
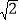 ,则它们组成一个等腰直角三角形;②两条对角线相等的平行四边形是矩形;③对角线互相垂直的四边形是菱形;④有两个角相等的梯形是等腰梯形;⑤一条直线与矩形的一组对边相交,必分矩形为两个直角梯形。
,则它们组成一个等腰直角三角形;②两条对角线相等的平行四边形是矩形;③对角线互相垂直的四边形是菱形;④有两个角相等的梯形是等腰梯形;⑤一条直线与矩形的一组对边相交,必分矩形为两个直角梯形。A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
-
科目: 来源: 题型:
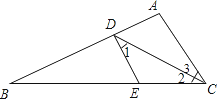
查看答案和解析>>【题目】如图,已知CD平分∠ACB,∠1=∠2.
(1)求证:DE∥AC;
(2)若∠3=30°,∠B=25°,求∠BDE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,延长BC到点D,连接OA,AD,使得∠FAC=∠AOD,∠D=∠BAF.

(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为5,CE=2,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,对角线AC和BD相交于O,∠AOB=60度,AC=10,(1)求矩形较短边的长.
(2)矩形较长边的长
(3)矩形的面积

如果把本题改为:矩形ABCD中,对角线AC和BD相交于O,∠AOB=60度,AB=4,你能求出这个矩形的面积吗?试写出解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,∠ABE与∠CDE的角平分线相交于点F,若∠F=125°,则∠E的度数为( )

A. 110° B. 120° C. 115° D. 105°
相关试题

