【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
参考答案:
【答案】C
【解析】
因为BC为AF边上的高,要求△AFC的面积,求得AF即可,先求证△AFD′≌△CFB,得BF=D′F,设D′F=BF=x,则在Rt△AFD′中,根据勾股定理列方程求出x即可得到结果.
解:由四边形ABCD为矩形以及折叠可得,AD′=AD=BC,∠D=∠D′=∠B,
又∠AFD′=∠CFB,
∴△AFD′≌△CFB(AAS),
∴D′F=BF,
设D′F=BF=x,则AF=8﹣x,
在Rt△AFD′中,(8﹣x)2=x2+42,
解得:x=3,
∴AF=8-x=8﹣3=5,
∴S△AFC=![]() AFBC=10.
AFBC=10.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A(0,m+4),点C(5m+3,0)在x轴的正半轴上,现将点C向左平移4单位长度再向上平移7个单位长度得到对应点B(7m﹣7,n).
(1)求m,n的值;
(2)若点P从点C出发以每秒2个单位长度/秒的速度沿CO方向移动,同时点Q从点O出发以每秒1个单位长度的速度沿OA方向移动,设移动的时间为t秒(0<t<7),四边形OPBA与△OQB的面积分别记为S1,S2.是否存在一段时间,使S1<2S2?若存在,求出t的取值范围;若不存在,试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,在平面直角坐标系中,点
,在平面直角坐标系中,点 ,
, 的坐标分别为
的坐标分别为 ,
, ,将线段
,将线段 先向上平移
先向上平移 个单位长度,再向右平移
个单位长度,再向右平移 个单位长度,得到线段
个单位长度,得到线段 ,连接
,连接 ,
, ,构成平行四边形
,构成平行四边形 .
. (1)请写出点
 的坐标为________,点
的坐标为________,点 的坐标为________,
的坐标为________, ________;
________;(2)点
 在
在 轴上,且
轴上,且 ,求出点
,求出点 的坐标;
的坐标;(3)如图
 ,点
,点 是线段
是线段 上任意一个点(不与
上任意一个点(不与 、
、 重合),连接
重合),连接 、
、 ,试探索
,试探索 、
、 、
、 之间的关系,并证明你的结论.
之间的关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
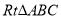 中,
中,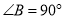 ,
, ,
, ,点
,点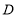 从点
从点 出发沿
出发沿 方向以每秒2个单位长度的速度向点
方向以每秒2个单位长度的速度向点 运动,同时点
运动,同时点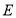 从点
从点 出发沿
出发沿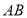 方向以每秒1个单位长度的速度向点
方向以每秒1个单位长度的速度向点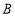 运动,当其中一个点到达终点时,另一个点也随之停止运动,设点
运动,当其中一个点到达终点时,另一个点也随之停止运动,设点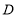 ,
,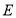 运动的时间是
运动的时间是 秒(
秒(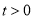 ).过点
).过点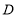 作
作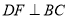 于点
于点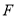 ,连接
,连接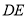 、
、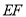 .
.
(1)求
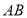 、
、 的长;
的长;(2)求证:
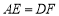 ;
;(3)四边形
 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的 值;如果不能,说明理由.
值;如果不能,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )

A.3
B.4
C.1
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 在直角坐标系中,
在直角坐标系中, 请写出
请写出 各点的坐标.
各点的坐标. 若把
若把 向上平移2个单位,再向左平移1个单位得到
向上平移2个单位,再向左平移1个单位得到 ,写出
,写出 、
、 、
、 的坐标,并在图中画出平移后图形.
的坐标,并在图中画出平移后图形. 求出三角形ABC的面积.
求出三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程变形正确的是( )
A.方程3x﹣2=2x﹣1移项,得3x﹣2x=﹣1﹣2
B.方程3﹣x=2﹣5(x﹣1)去括号,得3﹣x=2﹣5x﹣1
C.方程 可化为3x=6.
可化为3x=6.
D.方程 系数化为1,得x=﹣1
系数化为1,得x=﹣1
相关试题

