【题目】矩形ABCD中,对角线AC和BD相交于O,∠AOB=60度,AC=10,(1)求矩形较短边的长.
(2)矩形较长边的长
(3)矩形的面积

如果把本题改为:矩形ABCD中,对角线AC和BD相交于O,∠AOB=60度,AB=4,你能求出这个矩形的面积吗?试写出解答过程.
参考答案:
【答案】(1)较短边的长为5;(2)较长边的长是![]() ;(3)矩形的面积=
;(3)矩形的面积=![]()
变式答案:矩形ABCD的面积是![]() .
.
【解析】
(1)根据矩形的性质,可以得到△AOB是等边三角形,则可以求得OA的长,进而求得AB的长.
(2)在直角△ABC中,根据勾股定理来求BC的长度;
(3)由矩形的面积公式进行解答.
解:(1)∵四边形ABCD是矩形, ∴OA=OB
又∵∠AOB=60°,
∴△AOB是等边三角形.
∴AB=OA=![]() AC=5,
AC=5,
即矩形较短边的长为5;
(2)在直角△ABC中,∠ABC=90°,AB=5,AC=10,
则BC=![]()
即矩形较长边的长是![]() ;
;
(3)矩形的面积=ABBC=5×![]() =
=![]()

变式
解:在矩形ABCD中,AO=BO, 又∠AOB=60°,

∴△AOB是等边三角形.
∵△AOB是等边三角形
∴OA=OB=AB=4,
∴BD=2OB=8,
在Rt△ABD,AD=![]()
∴矩形ABCD的面积=![]()
答:矩形ABCD的面积是![]() .
.
-
科目: 来源: 题型:
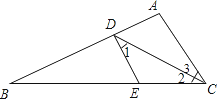
查看答案和解析>>【题目】如图,已知CD平分∠ACB,∠1=∠2.
(1)求证:DE∥AC;
(2)若∠3=30°,∠B=25°,求∠BDE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
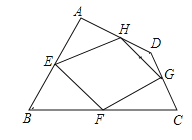
(1)四边形EFGH的形状是 ,证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,延长BC到点D,连接OA,AD,使得∠FAC=∠AOD,∠D=∠BAF.

(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为5,CE=2,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,∠ABE与∠CDE的角平分线相交于点F,若∠F=125°,则∠E的度数为( )

A. 110° B. 120° C. 115° D. 105°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长分别为
 和
和 的两个正方形
的两个正方形 和
和 并排放在一起,连结
并排放在一起,连结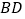 并延长交
并延长交 于点
于点 ,交
,交 于点
于点 ,则
,则


A.
 B. 2
B. 2 C. 2 D. 1
C. 2 D. 1 -
科目: 来源: 题型:
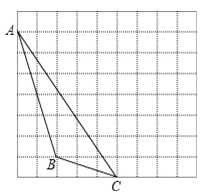
查看答案和解析>>【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上
(1)画出△ABC向右平移4格, 再向上平移1格后的△A1B1C1;
(2)图中BC与B1C1的关系是 ;
(3)图中△ABC的面积是
(4)请在AB上找一点D,使得线段CD平分△ABC的面积,在图上作出线段CD.
相关试题

