搜索
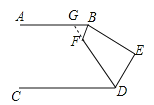
【题目】如图，已知AB∥CD，∠ABE与∠CDE的角平分线相交于点F，若∠F=125°，则∠E的度数为（ ）
A. 110° B. 120° C. 115° D. 105°
参考答案：
【答案】A
【解析】解：如图所示，延长DF与直线AB相交于点G．∵AB∥CD，∴∠FGB=∠CDF．∵∠BFD+∠GFB=180°，∠BFB=125°，∴∠GFB=55°．在三角形BFG中，∵∠BGF+∠GBF+∠GFB=180°，∴∠FGB+∠GBF=180°﹣55°=125°．∵∠ABE和∠CDE的平分线相交于点F，∴∠ABF=∠FBE，∠CDF=∠FDE，∴∠FGB=∠CDF=∠EDF，∴∠EDF+FBE=125°．∵四边形内角和为360°，∴∠E+∠DFB+∠EBF+∠EDF=360°，∴∠F=360°﹣125°﹣125°=110°．故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在平面直角坐标系中，直线l1的解析式为y=-x，直线l2与l1交于A点（a，-a）与，与y轴交于点B（0，b），其中a，b满足（a+2）2+
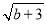=0 .(1)求直线l2放入解析式；
(2)在平面直角坐标系中第二象限有一点P（m，5），使得S△AOP=S△AOB，请求出点P的坐标；
(3)已知平行于y轴且位于y轴左侧有一动直线，分别与
， 
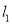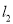交于点M、N，且点M在点N的下方，点Q为y轴上一动点，且△MNQ为等腰直角三角形，请直接写出满足条件的点Q的坐标.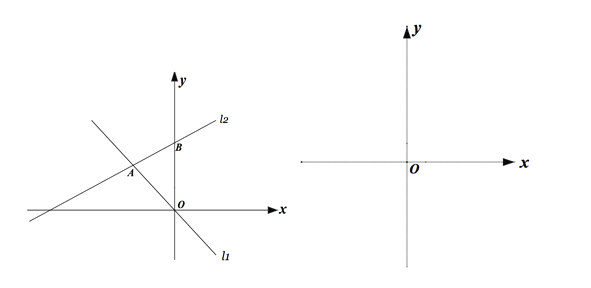 
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了考查一批日光灯管的使用寿命，从中抽取了100只日光灯管进行试验，在这个问题中，①总体是指这批日光灯管的全体；②个体是指每只日光灯管的使用寿命；③样本是指从中抽取的100只日光灯管的使用寿命；④样本容量是100只灯管，说法正确的有（ ）
A.1个B.2个C.3个D.4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了了解广大市民对垃圾分类知识的了解程度，应采用的合适的调查方式为_________．（填普查或抽样调查）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°，BC=8cm，AC=6cm，点E是BC的中点，动点P从A点出发，先以每秒2cm的速度沿A→C运动，然后以1cm/s的速度沿C→B运动．若设点P运动的时间是t秒，那么当t=_______，△APE的面积等于8．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将边长为12 cm的正方形ABCD沿其对角线AC剪开，再把ABC沿着AD方向平移，得到△A′B′C′，若两个三角形重叠部分的面积为32 cm2，则它移动的距离AA′等于( )
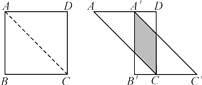
A. 4 cm B. 8 cm C. 6 cm D. 4 cm或8 cm
-
科目： 来源： 题型：
查看答案和解析>>【题目】操作示例：如图1，在△ABC中，AD为BC边上的中线，△ABD的面积记为S1，△ADC的面积记为S2．则S1=S2．
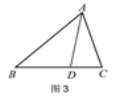
解决问题：在图2中，点D、E分别是边AB、BC的中点，若△BDE的面积为2，则四边形ADEC的面积为 .
拓展延伸：
（1）如图3，在△ABC中，点D在边BC上，且BD=2CD，△ABD的面积记为S1，△ADC的面积记为S2．则S1与S2之间的数量关系为 ．
（2）如图4，在△ABC中，点D、E分别在边AB、AC上，连接BE、CD交于点O，且BO=2EO，CO=DO，若△BOC的面积为3，则四边形ADOE的面积为 .
相关试题
