Question

【题目】如图所示，在以O为圆心的两个同心圆中，小圆的半径为1，AB与小圆相切于点A，与大圆相交于点B，大圆的弦BC⊥AB于点B，过点C作大圆的切线CD交AB的延长线于点D，连接OC交小圆于点E，连接BE、BO．
（1）求证：△AOB∽△BDC；
（2）设大圆的半径为x，CD的长为y： ①求y与x之间的函数关系式；
②当BE与小圆相切时，求x的值．

Answer 1

【答案】
（1）证明：

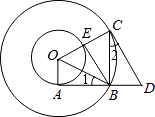
∵AB与小圆相切于点A，CD与大圆相切于点C，

∴∠OAB=∠OCD=90°，

∵BC⊥AB，

∴∠CBA=∠CBD=90°，

∵∠1+∠OBC=90°，∠2+∠OCB=90°，

又∵OC=OB，

∴∠OBC=∠OCB，

∴∠1=∠2，

∴△AOB∽△BDC

（2）解：

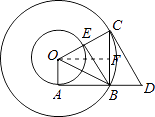
①过点O作OF⊥BC于点F，则四边形OABF是矩形，

∴BF=OA=1，

由垂径定理，得BC=2BF=2，

在Rt△AOB中，OA=1，OB=x

∴AB= ，

由（1）得△AOB∽△BDC

∴ ，即 ，

∴y= ；

②当BE与小圆相切时，OE⊥BE，

∵OE=1，OC=x，

∴EC=x﹣1，BE=AB= ，

在Rt△BCE中，根据勾股定理得：EC2+BE2=BC2，

即（x﹣1）2+（ ）2=22，

解得：x1=2，x2=﹣1（舍去），

∴当BE与小圆相切时，x=2．

【解析】（1）由AB与小圆相切，CD与大圆相切，根据切线性质可得∠OAB与∠OCD相等，都为直角，又BC与AB垂直，根据垂直定义得到∠CBA与∠CBD都为直角，则∠1+∠OBC与∠2+∠OCB和都为90°，由OC=OB，根据“等边对等角”得到∠OBC=∠OCB，根据等角的余角相等，得到∠1=∠2，由两对对应角相等的两三角形相似得证；（2）①过O作OF垂直于BC，由三个角都为直角的四边形为矩形得到ABOF为矩形，根据矩形的对边相等，得到FB=OA，由OA的长得到FB的长，又BC为大圆的弦，利用垂径定理得到BC=2BF，从而求出BC的长，在直角三角形OAB中，由OA=1，OB=x，利用勾股定理表示出AB，由（1）得到的三角形相似得比例，把相应的值代入即可得到y与x的关系式；②当BE与小圆相切时，根据切线性质得到OE与BE垂直，由OE和OC表示出EC的长，根据切线长定理得到BE=BA，表示出EB，在直角三角形ECB中，由EC，EB及BC的长，利用勾股定理列出关于x的方程，求出方程的解即可得到x的值．
【考点精析】根据题目的已知条件，利用勾股定理的概念和垂径定理的相关知识可以得到问题的答案，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．