【题目】如图,已知F是以AC为直径的半圆O上任意一点,过AC上任意一点H作AC的垂线分别交CF,AF的延长线于点E,B,点D是线段BE的中点.
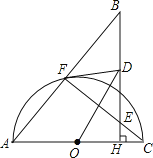
(1)求证:DF是⊙O的切线;
(2)若BF=AF,求证AF2=EF·CF.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】分析:(1)连接OF,根据圆周角定理得出∠AFC=90°,然后根据直角三角形斜边中线的性质求得DF=DE=![]() BE,根据等边对等角得出∠1=∠2,∠3=∠C,进而求得OF⊥DF,即可证得DF是 O的切线.(2)由∠C=∠BEF,∠EFB=∠AFC,可推出△EFB∽△AFC,进而推出
BE,根据等边对等角得出∠1=∠2,∠3=∠C,进而求得OF⊥DF,即可证得DF是 O的切线.(2)由∠C=∠BEF,∠EFB=∠AFC,可推出△EFB∽△AFC,进而推出![]() ,即可求解.
,即可求解.
本题解析:1)证明:如图1,连接OF,
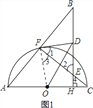
∵AC是直径∴∠AFC=90°∴∠BFE=90°,
∵D是BE的中点∴DF=DE=![]() BE,∴∠1=∠2,
BE,∴∠1=∠2,
∵OF=OC,∴∠3=∠C,∴∠1+∠3=∠2+∠C=∠4+∠C,
∵BH⊥AC,∴在Rt△ECH中,∠4+∠C=90°,
∴∠1+∠3=90°,∴∠DFO=90°,∴OF⊥DF,
∴DF是O的切线。
(2)∵∠C=∠BEF,∠EFB=∠AFC, ∴△EFB∽△AFC,∴![]() ,即AF·BF= EF·CF,又BF=AF,∴AF2=EF·CF.
,即AF·BF= EF·CF,又BF=AF,∴AF2=EF·CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC,若三角形ABC的边长为1,AE=2,则CD的长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式的计算,正确的是( )
A. 3a+2b=5abB. 5y2﹣3y2=2
C. ﹣12x+7x=﹣5xD. 4m2n﹣2mn2=2mn
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定运算符号的意义是:当a>b时,ab=a﹣b;当a<b时,ab=a+b.
(1)计算:61= ;(﹣3)2= ;
(2)棍据运算符号的意义且其他运算符号意义不变的条件下,
①计算:﹣14+15×[(﹣
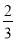 )(﹣
)(﹣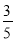 )]﹣(3223)÷(﹣7),
)]﹣(3223)÷(﹣7),②若x,y在数轴上的位置如图所示,
a.填空:x2+1 y(填“>“或“<”):
b.化简:[(x2+x+1)(x+y)]+[(y﹣x2)(y+2)].

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A. 9的平方根是﹣3B. ﹣7是﹣49的平方根
C. ﹣5是-125的立方根D. 8的立方根是±2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.
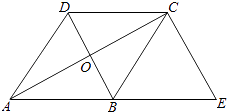
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校礼堂前4排共有(6a+3b+10)个座位,第1排有a个座位,第2排座位数比第3排座数的
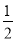 多5个,第3排座位数比第1排座位的2倍多6个.
多5个,第3排座位数比第1排座位的2倍多6个.(1)求第3排的座位数(用含a,b的式子表示):
(2)求第4排的座位数(用含a,b的式子表示):
(3)若前4排共有82个座位,求第3排比第2排多多少个座位.
相关试题

