搜索
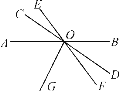
【题目】如图，直线AB，CD，EF相交于点O，OG是∠AOF的平分线，∠BOD＝35°，∠COE＝18°，则∠COG的度数是________．
参考答案：
【答案】98.5°
【解析】
已知∠BOD、∠COE的度数，根据对顶角相等可求出∠AOC、∠DOF的度数，∠BOD已知，∠DOF已求出，则∠AOF的度数可求出，再根据OG 是∠AOF的平分线，进一步求出∠AOG，再根据∠COG=∠AOC+∠AOG，则∠COG的度数即可求得.
∵∠BOD=35°，
∴∠AOC=35°，
∵∠COE=18°，
∴∠DOF=18°，
∴∠BOF=∠BOD+∠DOF=35°+18°=53°，
∴∠AOF=180°－53°=127°，
∵OG平分∠AOF，
∴∠AOG=∠GOF=
∠AOF=×127°=63.5°，
∴∠COG=∠AOC+∠AOG=35°+63.5°=98.5°.
故答案为：98.5°
-
科目： 来源： 题型：
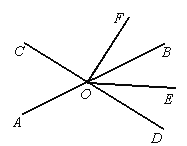
查看答案和解析>>【题目】如图，直线AB、CD相交于点O，∠AOD＝120°，FO⊥OD，OE平分∠BOD．
（1）求∠EOF的度数；
（2）试说明OB平分∠EOF．
-
科目： 来源： 题型：
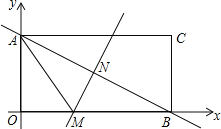
查看答案和解析>>【题目】如图，长方形AOBC在直角坐标系中，点A在y轴上，点B在x轴上，已知点C的坐标是（8，4）．
（1）对角线AB的垂直平分线MN交x轴于点M，连接AM，求线段AM的长；
（2）在x轴上是否存在一个点P，使△PAM为等腰三角形？如果有请直接写出符合题意的所有点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读与理解： 图1是边长分别为a和b（a＞b）的两个等边三角形纸片ABC和C′DE叠放在一起（C与C′重合）的图形．
操作与证明：
（1）操作：固定△ABC，将△C′DE绕点C按顺时针方向旋转30°，连接AD，BE，如图2；在图2中，线段BE与AD之间具有怎样的大小关系？证明你的结论；
（2）操作：若将图1中的△C′DE，绕点C按顺时针方向任意旋转一个角度α，连接AD，BE，如图3；在图3中，线段BE与AD之间具有怎样的大小关系？证明你的结论；
猜想与发现：
根据上面的操作过程，请你猜想当α为多少度时，线段AD的长度最大是多少？当α为多少度时，线段AD的长度最小是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC的三边AB、BC、CA长分别是20、30、40，其三条角平分线将△ABC分为三个三角形，则S△ABO︰S△BCO︰S△CAO等于（ ）
A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察，在如图所示的各图中找对顶角（不含平角）：
（1）如图a，图中共有_____对对顶角．
（2）如图b，图中共有_____对对顶角．
（3）如图c，图中共有_____对对顶角
（4）研究（1）～（3）小题中直线条数与对顶角的对数之间的关系，若有n条直线相交于一点，则可形成多少对对顶角？
（5）若有2000条直线相交于一点，则可形成多少对对顶角？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y1=a（x+2）2﹣3与y2=
（x﹣3）2+1交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．则以下结论： ①无论x取何值，y2的值总是正数；
②a=1；
③当x=0时，y2﹣y1=4；
④2AB=3AC；
其中正确结论是（ ）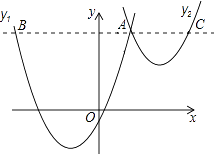
A.①②
B.②③
C.③④
D.①④
相关试题
