【题目】如图,抛物线y1=a(x+2)2﹣3与y2= ![]() (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论: ①无论x取何值,y2的值总是正数;
(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论: ①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2﹣y1=4;
④2AB=3AC;
其中正确结论是( )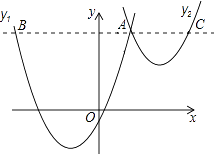
A.①②
B.②③
C.③④
D.①④
参考答案:
【答案】D
【解析】解:①∵抛物线y2= ![]() (x﹣3)2+1开口向上,顶点坐标在x轴的上方,∴无论x取何值,y2的值总是正数,故本小题正确;②把A(1,3)代入,抛物线y1=a(x+2)2﹣3得,3=a(1+2)2﹣3,解得a=
(x﹣3)2+1开口向上,顶点坐标在x轴的上方,∴无论x取何值,y2的值总是正数,故本小题正确;②把A(1,3)代入,抛物线y1=a(x+2)2﹣3得,3=a(1+2)2﹣3,解得a= ![]() ,故本小题错误;③由两函数图象可知,抛物线y1=a(x+2)2﹣3解析式为y1=
,故本小题错误;③由两函数图象可知,抛物线y1=a(x+2)2﹣3解析式为y1= ![]() (x+2)2﹣3,当x=0时,y1=
(x+2)2﹣3,当x=0时,y1= ![]() (0+2)2﹣3=﹣
(0+2)2﹣3=﹣ ![]() ,y2=
,y2= ![]() (0﹣3)2+1=
(0﹣3)2+1= ![]() ,故y2﹣y1=
,故y2﹣y1= ![]() +
+ ![]() =
= ![]() ,故本小题错误;④∵物线y1=a(x+2)2﹣3与y2=
,故本小题错误;④∵物线y1=a(x+2)2﹣3与y2= ![]() (x﹣3)2+1交于点A(1,3), ∴y1的对称轴为x=﹣2,y2的对称轴为x=3,
(x﹣3)2+1交于点A(1,3), ∴y1的对称轴为x=﹣2,y2的对称轴为x=3,
∴B(﹣5,3),C(5,3)
∴AB=6,AC=4,
∴2AB=3AC,故本小题正确.
故选D.
根据与y2= ![]() (x﹣3)2+1的图象在x轴上方即可得出y2的取值范围;把A(1,3)代入抛物线y1=a(x+2)2﹣3即可得出a的值;由抛物线与y轴的交点求出,y2﹣y1的值;根据两函数的解析式直接得出AB与AC的关系即可.
(x﹣3)2+1的图象在x轴上方即可得出y2的取值范围;把A(1,3)代入抛物线y1=a(x+2)2﹣3即可得出a的值;由抛物线与y轴的交点求出,y2﹣y1的值;根据两函数的解析式直接得出AB与AC的关系即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD,EF相交于点O,OG是∠AOF的平分线,∠BOD=35°,∠COE=18°,则∠COG的度数是________.
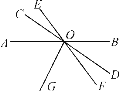
-
科目: 来源: 题型:
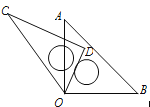
查看答案和解析>>【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察,在如图所示的各图中找对顶角(不含平角):

(1)如图a,图中共有_____对对顶角.
(2)如图b,图中共有_____对对顶角.
(3)如图c,图中共有_____对对顶角
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成多少对对顶角?
(5)若有2000条直线相交于一点,则可形成多少对对顶角?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将一副直角三角板的顶点叠合在一起,记为点O(∠C=30°,∠A=45°).
(1)当∠AOC=45°时,求∠DOB的度数;
(2)请探究∠AOC和∠DOB之间满足的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直线1上依次摆放着四个正方形和三个等腰直角三角形(阴影图形),已知三个等腰直角三角形的面积从左到右分别为1、2、3,四个正方形的面积从左到右依次是S1、S2、S3、S4,则S1+S2+S3+S4的值为( )

A. 4 B. 5 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有A, B两点,分别表示的数为
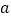 ,
, ,且
,且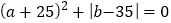 .点P从A点出发以每秒13个单位长度的速度沿数轴向右匀速运动,当它到达B点后立即以相同的速度返回往A点运动,并持续在A,B两点间往返运动.在点P出发的同时,点Q从B点出发以每秒2个单位长度向左匀速运动,当点Q达到A点时,点P,Q停止运动.
.点P从A点出发以每秒13个单位长度的速度沿数轴向右匀速运动,当它到达B点后立即以相同的速度返回往A点运动,并持续在A,B两点间往返运动.在点P出发的同时,点Q从B点出发以每秒2个单位长度向左匀速运动,当点Q达到A点时,点P,Q停止运动.(1)填空:
 ,
,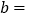 ;
;(2)求运动了多长时间后,点P,Q第一次相遇,以及相遇点所表示的数;
(3)求当点P,Q停止运动时,点P所在的位置表示的数;
(4)在整个运动过程中,点P和点Q一共相遇了几次.(直接写出答案)


相关试题

