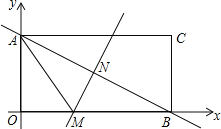
【题目】如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x轴上,已知点C的坐标是(8,4).
(1)对角线AB的垂直平分线MN交x轴于点M,连接AM,求线段AM的长;
(2)在x轴上是否存在一个点P,使△PAM为等腰三角形?如果有请直接写出符合题意的所有点P的坐标.
参考答案:
【答案】(1)AM=5;(2)△PAM为等腰三角形,点P的坐标是(-3,0)或(-2,0)或(8,0或(-![]() ,0).
,0).
【解析】
(1)设AM=x,则BM=x,OM=8-x,根据勾股定理列方程得:AO2+OM2=AM2,则42+(8-x)2=x2,解出即可;
(2)△PAM为等腰三角形时,分情况进行讨论:①以A为圆心,以AM为半径画圆;②以M为圆心,以MA为半径,画圆;③作AM的垂直平分线;确定点P的位置,分别计算可得结论.
(1)由题意得:OA=4,OB=8,
∵MN是AB的垂直平分线,
∴AM=BM,
设AM=x,则BM=x,OM=8-x,
Rt△AOM中,由勾股定理得:AO2+OM2=AM2,
∴42+(8-x)2=x2,
解得:x=5,
∴AM=5;
(2)如图,①当AP1=AM=5时,OM=OP1=3,此时P1(-3,0);
②当AM=P2M=P3M=5时,此时P2(-2,0),P3(8,0);

③如图,作AM的垂直平分线,交AM于E,交x轴于P4,
∴EM=![]() ,
,
sin∠EP4M=![]() =sin∠OAM=
=sin∠OAM=![]() ,
,
∴P4M=![]() ,
,
∴OP4=![]() -3=
-3=![]() ,此时P4(-
,此时P4(-![]() ,0),
,0),
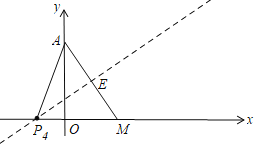
综上,△PAM为等腰三角形,点P的坐标是(-3,0)或(-2,0)或(8,0)或(-![]() ,0)
,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣
 ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)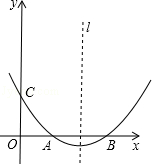
(1)求抛物线的解析式及A,B两点的坐标;
(2)若(1)中抛物线的对称轴上有点P,使△ABP的面积等于△ABC的面积的2倍,求出点P的坐标;
(3)在(1)中抛物线的对称轴l上是否存在一点Q,使AQ+CQ的值最小?若存在,求AQ+CQ的最小值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】以下列数组作为三角形的三条边长,其中能构成直角三角形的是( )
A. 1,
 ,3 B.
,3 B.  ,
,  ,5 C. 1.5,2,2.5 D.
,5 C. 1.5,2,2.5 D.  ,
,  ,
, 
【答案】C
【解析】A、12+(
 )2≠32,不能构成直角三角形,故选项错误;
)2≠32,不能构成直角三角形,故选项错误;B、(
 2+(
2+( )2≠52,不能构成直角三角形,故选项错误;
)2≠52,不能构成直角三角形,故选项错误;C、1.52+22=2.52,能构成直角三角形,故选项正确;
D、(
 ))2+(
))2+( )2≠(
)2≠( )2,不能构成直角三角形,故选项错误.
)2,不能构成直角三角形,故选项错误.故选:C.
【题型】单选题
【结束】
3【题目】在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到斜边AB的距离是( )
(A)
 (B)
(B) (C)9 (D)6
(C)9 (D)6 -
科目: 来源: 题型:
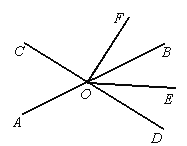
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠AOD=120°,FO⊥OD,OE平分∠BOD.
(1)求∠EOF的度数;
(2)试说明OB平分∠EOF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与理解: 图1是边长分别为a和b(a>b)的两个等边三角形纸片ABC和C′DE叠放在一起(C与C′重合)的图形.

操作与证明:
(1)操作:固定△ABC,将△C′DE绕点C按顺时针方向旋转30°,连接AD,BE,如图2;在图2中,线段BE与AD之间具有怎样的大小关系?证明你的结论;
(2)操作:若将图1中的△C′DE,绕点C按顺时针方向任意旋转一个角度α,连接AD,BE,如图3;在图3中,线段BE与AD之间具有怎样的大小关系?证明你的结论;
猜想与发现:
根据上面的操作过程,请你猜想当α为多少度时,线段AD的长度最大是多少?当α为多少度时,线段AD的长度最小是多少? -
科目: 来源: 题型:
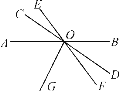
查看答案和解析>>【题目】如图,直线AB,CD,EF相交于点O,OG是∠AOF的平分线,∠BOD=35°,∠COE=18°,则∠COG的度数是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
相关试题

