【题目】如图在下面平面直角坐标系中,已知A ![]() ,B
,B ![]() ,C
,C ![]() 三点.其中
三点.其中![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)如果在第二象限内有一点![]()
![]() ,请用含
,请用含![]() 的式子表示四边形
的式子表示四边形![]() 的面积;
的面积;
(3)在(2)的条件下,是否存在点![]() ,使四边形
,使四边形![]() 的面积为△
的面积为△![]() 的面积的两倍?若存在,求出点
的面积的两倍?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

参考答案:
【答案】(1)a=2,b=3,c=4;(2)四边形ABOP的面积为3-m;(3)存在,点P坐标为![]()
【解析】分析:(1)根据几个非负数和的性质得到a-2=0,b-3=0,c-4=0,分别解一元一次方程得到a=2,b=3,b=4;
(2)根据三角形的面积公式和四边形ABOP的面积=S△AOP+S△AOB进行计算;
(3)若S四边形ABOP≥S△AOP,则-m+3≥2×![]() ×2×(-m),解得m≥-3,则m=-1,-2,-3,然后分别写出P点的坐标.
×2×(-m),解得m≥-3,则m=-1,-2,-3,然后分别写出P点的坐标.
详解:(1)∵|a-2|+(b-3)2+![]() =0,
=0,
∴a-2=0,b-3=0,c-4=0,
∴a=2,b=3,b=4;
(2)A点坐标为(0,2),B点坐标为(3,0),
四边形ABOP的面积=S△AOP+S△AOB
=![]() ×2×(-m)+
×2×(-m)+![]() ×2×3
×2×3
=-m+3;
(3)存在.理由如下:
∵S四边形ABOP≥S△AOP,
∴-m+3≥2×![]() ×2×(-m),
×2×(-m),
∴m≥-3,
∵m为负整数,
∴m=-1,-2,-3,
∴点P的坐标为(-1,![]() )或(-2,
)或(-2,![]() )或(-3,
)或(-3,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各多少万元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元. 则有哪几种购车方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】两条直线y1=ax+b与y2=bx+a(a≠0,b≠0)在同一平面直角坐标系中的图象可能是( )
A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在菱形ABCD中,∠B=∠EAF=60°,∠BAE=20°,则∠AEF的大小是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是高,CE是中线,点G是CE的中点,且DG⊥CE,垂足为点G.
(1)求证:DC=BE;
(2)若∠AEC=54°,求∠BCE的度数.

-
科目: 来源: 题型:
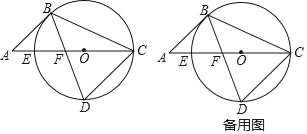
查看答案和解析>>【题目】如图,已知CE是圆O的直径,点B在圆O上由点E顺时针向点C运动(点B不与点E、C重合),弦BD交CE于点F,且BD=BC,过点B作弦CD的平行线与CE的延长线交于点A.
(1)若圆O的半径为2,且点D为弧EC的中点时,求圆心O到弦CD的距离;
(2)当DFDB=CD2时,求∠CBD的大小;
(3)若AB=2AE,且CD=12,求△BCD的面积.
相关试题

