【题目】在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.

参考答案:
【答案】(1)证明见解析(2)菱形
【解析】
(1)根据正方形的性质和全等三角形的判定证明即可;
(2)四边形AECF是菱形,根据对角线垂直的平行四边形是菱形即可判断;
详证明:(1)∵四边形ABCD是正方形,
∴AB=AD,
∴∠ABD=∠ADB,
∴∠ABE=∠ADF,
在△ABE与△ADF中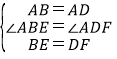 ,
,
∴△ABE≌△ADF.
(2)如图,连接AC,
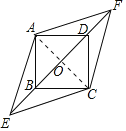
四边形AECF是菱形.
理由:在正方形ABCD中,
OA=OC,OB=OD,AC⊥EF,
∴OB+BE=OD+DF,
即OE=OF,
∵OA=OC,OE=OF,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴四边形AECF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两条直线y1=ax+b与y2=bx+a(a≠0,b≠0)在同一平面直角坐标系中的图象可能是( )
A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在菱形ABCD中,∠B=∠EAF=60°,∠BAE=20°,则∠AEF的大小是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在下面平面直角坐标系中,已知A
 ,B
,B  ,C
,C  三点.其中
三点.其中 满足
满足 .
.(1)求
 的值;
的值;(2)如果在第二象限内有一点

 ,请用含
,请用含 的式子表示四边形
的式子表示四边形 的面积;
的面积;(3)在(2)的条件下,是否存在点
 ,使四边形
,使四边形 的面积为△
的面积为△ 的面积的两倍?若存在,求出点
的面积的两倍?若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是高,CE是中线,点G是CE的中点,且DG⊥CE,垂足为点G.
(1)求证:DC=BE;
(2)若∠AEC=54°,求∠BCE的度数.

-
科目: 来源: 题型:
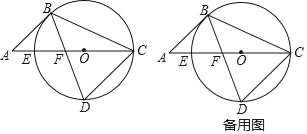
查看答案和解析>>【题目】如图,已知CE是圆O的直径,点B在圆O上由点E顺时针向点C运动(点B不与点E、C重合),弦BD交CE于点F,且BD=BC,过点B作弦CD的平行线与CE的延长线交于点A.
(1)若圆O的半径为2,且点D为弧EC的中点时,求圆心O到弦CD的距离;
(2)当DFDB=CD2时,求∠CBD的大小;
(3)若AB=2AE,且CD=12,求△BCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥CD,EF交AB于E,交CD于F,∠AEF=68°,FG平分∠EFD,KF⊥FG,求∠KFC的度数.

解:∵AB∥CD(已知)
∴∠EFD=∠AEF( )
∵∠AEF=68°(已知)
∴∠EFD=∠AEF=68°( )
∵FG平分∠EFD(已知)
所以∠EFG=∠GFD=
 ∠EFD=34°( )
∠EFD=34°( )又因为KF⊥FG( )
所以∠KFG=90°( )
所以∠KFC=180°-∠GFD-∠KFG= .
相关试题

