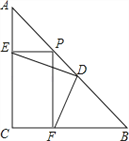
【题目】在△ABC中,∠C=90°,AC=BC=3,D为AB的中点,点P是AB上的一个动点,PE⊥AC于点E,PF⊥BC于点F.
(1)求证:AE=PE;
(2)求证:DE=DF;
(3)连接EF,EF的最小值是多少?
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】分析:(1)证明△AEP是等腰直角三角形;(2)连接CD,用SAS证明△AED≌△CFD;(3)利用CP=EF,即为求CP的最小值,当CP⊥AB时,CP取最小值.
详解:(1)∵∠C=90°,AC=BC,∴∠CAB=45°.
∵PE⊥AC,∴∠AEP=90°,∴∠APE=90°-45°=45°,
∴∠EAP=∠APE,∴AE=EP.
(2)连接CD,
∵∠C=90°,D为AB的中点,∴CD=AD.
∵AC=BC,∴∠DCF=45°,∴∠A=∠FCD,
∵PE⊥AC,PF⊥BC,∴∠CEP=∠CFP=90°,
∴四边形CEPF是矩形,∴PE=CF,∴AE=CF,
∴△AED≌△CFD(SAS),∴DE=DF.
(3)∵四边形CEPF是矩形,所以EF=CP.
∴EF最小时,CP也最小.
由垂线段最短得,当CP⊥AB时,CP最短,此时,点P与点D重合.
∵△ACP是等腰直角形,∴CP=![]() .
.
则EF的最小值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七
 班派出
班派出 名同学参加数学竞赛,老师以
名同学参加数学竞赛,老师以 分为基准,把分数超过
分为基准,把分数超过 分的部分记为正数,不足部分记为负数.评分记录如下:
分的部分记为正数,不足部分记为负数.评分记录如下: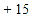 ,
,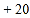 ,
, ,
,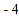 ,
,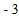 ,
, ,
,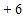 ,
,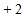 ,
, ,
,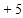 ,
,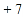 ,
,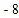 .
. 这
这 名同学中最高分和最低分各是多少?
名同学中最高分和最低分各是多少? 超过基准分的和低于基准分的各有多少人?
超过基准分的和低于基准分的各有多少人? 这十二名同学的平均成绩是多少?
这十二名同学的平均成绩是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的
 方阵图中,处于同一横行、同一竖列、同一斜对角线上的
方阵图中,处于同一横行、同一竖列、同一斜对角线上的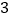 个数之和都相等.现在方阵图中已填写了一些数和代数式(其中每个代数式都表示一个数),则
个数之和都相等.现在方阵图中已填写了一些数和代数式(其中每个代数式都表示一个数),则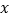 的值为________,
的值为________,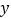 的值为________,空白处应填写的
的值为________,空白处应填写的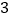 个数的和为________.
个数的和为________.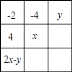
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂对一批袋装食盐抽样检查,共抽取了20袋,假设标准质量为120g,超出的部分记为“+”,不足的部分记为“-”,则这20袋食盐对应的数据如下表所示(单位:g):
与标准质量的差值
-4
-2
-1
0
+0.5
+1.5
+2.5
袋数
1
2
3
6
4
2
2
(1)若合格标准为“120g
 2g”,试求这一批食盐的合格率;
2g”,试求这一批食盐的合格率;(2)试求这20袋食盐的总质量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在矩形ABCD中,AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.
(1)求矩形ABCD的面积;
(2)求第1个平行四边形OBB1C的面积是
第2个平行四边形A1B1C1C是
第3个平行四边形O1B1B2C1的面积是
(3)求第n个平行四边形的面积是

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学兴趣小组开展了一次课外活动,过程如下:
如图①,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合,三角板的一边交AB于点P,另一边交BC的延长线于点Q.

(1)求证:AP=CQ;
(2)如图②,小明在图①的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并证明.
(3)如图③,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC的延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△ DEQ的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,若∠ABC的平分线把边AD分成长是2cm和3cm的两条线段,求□ABCD的周长.
相关试题

