【题目】某校为了解学生每天参加户外活动的情况,随机抽查了100名学生每天参加户外活动的时间情况,并将抽查结果绘制成如图所示的扇形统计图.
请你根据图中提供的信息解答下列问题:

(1)请直接写出图中![]() 的值,并求出本次抽查中学生每天参加户外活动时间的中位数;
的值,并求出本次抽查中学生每天参加户外活动时间的中位数;
(2)求本次抽查中学生每天参加户外活动的平均时间.
参考答案:
【答案】(1)a=20%.本次抽查中学生每天参加活动时间的中位数是1;
(2)本次抽查中学生每天参加户外活动的平均时间是1.175小时.
【解析】
试题分析:(1)用1减去其它组的百分比即可求得a的值,然后求得各组的人数,根据中位数定义求得中位数;
(2)利用加权平均数公式即可求解.
试题解析:(1)a=1﹣15%﹣25%﹣40%=20%.
100×20%=20(人),
100×40%=40(人),
100×25%=25(人),
100×15%=15(人).
则本次抽查中学生每天参加活动时间的中位数是1;
(2)![]() =1.175(小时).
=1.175(小时).
答:本次抽查中学生每天参加户外活动的平均时间是1.175小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,点A的坐标为(﹣2,3),下列说法正确的是( )
A. 点A与点B(2,﹣3)关于x轴对称
B. 点A与点C(﹣3,﹣2)关于x轴对称
C. 点A与点D(2,3)关于y轴对称
D. 点A与点E(3,2)关于y轴对称
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 的一元二次方程
的一元二次方程 .
.(1)当
 为何值时,方程有两个不相等的实数根?
为何值时,方程有两个不相等的实数根?(2)若边长为5的菱形的两条对角线的长分别为方程两根的2倍,求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)a(1﹣a)+(a+1)2﹣1
(2)(2y﹣z)2﹣(z+2y)(2y﹣z) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图中的图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:

①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为 千米/时;
千米/时;
④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.
其中正确的说法共有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图4,在平面直角坐标系中2条直线为
 ,
,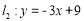 ,直线
,直线 交
交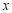 轴于点
轴于点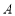 ,交
,交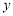 轴于点
轴于点 ,直线
,直线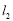 交
交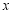 轴于点
轴于点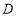 ,过点
,过点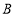 作
作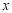 轴的平行线交
轴的平行线交 于点
于点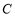 ,点
,点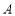 、
、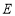 关于
关于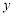 轴对称,抛物线
轴对称,抛物线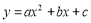 过
过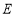 、
、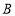 、
、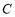 三点,下列判断中:
三点,下列判断中:①
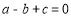 ;
;②
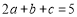 ;
;③抛物线关于直线
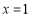 对称;
对称;④抛物线过点
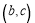 ;
;⑤
 ,其中正确的个数有( )
,其中正确的个数有( )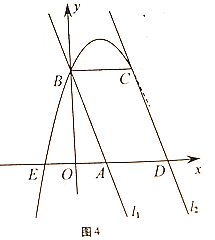
A.5 B.4 C.3 D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1、x2为一元二次方程x2﹣bx﹣3=0的两个实数根,且x1+x2=2,则( )
A.x1=1,x2=3B.x1=﹣1,x2=﹣3
C.x1=1,x2=﹣3D.x1=﹣1,x2=3
相关试题

