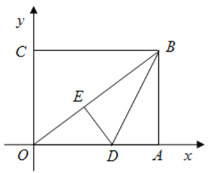
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() 、
、![]() ,将矩形
,将矩形![]() 的一个角沿直线
的一个角沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 轴交于点
轴交于点![]() .
.
(1)求线段![]() 的长度;
的长度;
(2)求直线![]() 所对应的函数表达式;
所对应的函数表达式;
(3)若点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形?若存在,请求出点
为顶点的四边形是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)15;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据勾股定理即可解决问题;
(2)设AD=x,则OD=OA=AD=12-x,根据轴对称的性质,DE=x,BE=AB=9,又OB=15,可得OE=OB-BE=15-9=6,在Rt△OED中,根据OE2+DE2=OD2,构建方程即可解决问题;
(3)过点E作EP∥BD交BC于点P,过点P作PQ∥DE交BD于点Q,则四边形DEPQ是平行四边形,再过点E作EF⊥OD于点F,想办法求出最小PE的解析式即可解决问题.
解:(1)由题知:![]() .
.
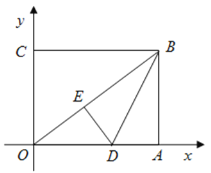
(2)设![]() ,则
,则![]() ,
,
根据轴对称的性质,![]() ,
,![]() ,
,
又![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
解得 ![]() ,
,
∴![]() ,
,
∴点![]() ,
,
设直线![]() 所对应的函数表达式为:
所对应的函数表达式为:![]() ,
,
则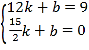 , 解得
, 解得![]() ,
,
∴直线![]() 所对应的函数表达式为:
所对应的函数表达式为:![]() ,
,
(3)存在,过点![]() 作EP∥DB交
作EP∥DB交![]() 于点
于点![]() ,过点
,过点![]() 作PQ∥ED交
作PQ∥ED交![]() 于点
于点![]() ,则四边形
,则四边形![]() 是平行四边形.再过点
是平行四边形.再过点![]() 作
作![]() 于点
于点![]() ,
,
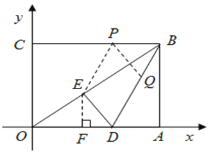
由![]() ,
,
得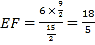 ,即点
,即点![]() 的纵坐标为
的纵坐标为![]() ,
,
又点![]() 在直线
在直线![]() :
:![]() 上,
上,
∴![]() , 解得
, 解得 ![]() , ∴
, ∴![]()
由于EP∥DB,所以可设直线![]() :
:![]() ,
,
∵![]() 在直线
在直线![]() 上
上
∴![]() , 解得
, 解得 ![]() ,
,
∴直线![]() :
:![]() ,
,
令![]() ,则
,则![]() ,
,
解得![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店计划购进A、B两种型号的电动自行车共30辆,其中A型电动自行车不少于20辆,A、B两种型号电动自行车的进货单价分别为2500元、3000元,售价分别为2800元、3500元,设该商店计划购进A型电动自行车m辆,两种型号的电动自行车全部销售后可获利润y元.
(1)求出y与m之间的函数关系式;
(2)该商店如何进货才能获得最大利润?此时最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合实践
问题情景:某综合实践小组进行废物再利用的环保小卫士行动. 他们准备用废弃的宣传单制作装垃圾的无盖纸盒.
操作探究:
⑴若准备制作一个无盖的正方体形纸盒,如图1,下面的哪个图形经过折叠能围成无盖正方体形纸盒?

⑵如图2是小明的设计图,把它折成无盖正方体形纸盒后与“保”字相对的是哪个字?
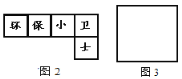
⑶如图3,有一张边长为20cm的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无盖长方体形纸盒.
①请你在图3中画出示意图,用实线表示剪切线,虚线表示折痕.
②若四角各剪去了一个边长为xcm的小正方形,用含x的代数式表示这个纸盒的高为 cm,底面积为 cm2,当小正方形边长为4cm时,纸盒的容积为 cm3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)求从袋中随机摸出一球,标号是1的概率;
(2)从袋中随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的有( )
①用两颗钉子就可以把木条固定在墙上
②把笔尖看成一个点,当这个点运动时便得到一条线;
③把弯曲的公路改直,就能缩短路程;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上。
A.
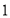 个B.
个B. 个C.
个C. 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B两点在数轴上,点A在原点O的左边,表示的数为﹣10,点B在原点的右边,且BO=3AO.点M以每秒3个单位长度的速度从点A出发向右运动.点N以每秒2个单位长度的速度从点O出发向右运动(点M,点N同时出发).
(1)数轴上点B对应的数是 ,点B到点A的距离是 ;
(2)经过几秒,原点O是线段MN的中点?
(3)经过几秒,点M,N分别到点B的距离相等?

-
科目: 来源: 题型:
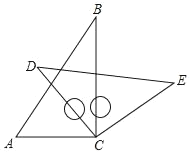
查看答案和解析>>【题目】将一副三角板中的两块直角板中的两个直角顶点重合在一起,即按如图所示的方式叠放在一起,其中∠A=60°,∠B=30,∠D=45°.
(1)若∠BCD=45°,求∠ACE的度数.
(2)若∠ACE=150°,求∠BCD的度数.
(3)由(1)、(2)猜想∠ACE与∠BCD存在什么样的数量关系并说明理由.
相关试题

