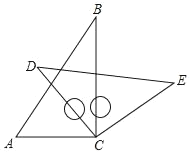
【题目】将一副三角板中的两块直角板中的两个直角顶点重合在一起,即按如图所示的方式叠放在一起,其中∠A=60°,∠B=30,∠D=45°.
(1)若∠BCD=45°,求∠ACE的度数.
(2)若∠ACE=150°,求∠BCD的度数.
(3)由(1)、(2)猜想∠ACE与∠BCD存在什么样的数量关系并说明理由.
参考答案:
【答案】(1)∠ACE=135°;(2)∠BCD=30°;(3)∠ACE与∠BCD互补.理由见解析.
【解析】
(1)先求得∠ACD的度数,即可得到∠ACE的度数;
(2)先求得∠ACD的度数,即可得到∠BCD的度数;
(3)依据∠BCD=∠ACB﹣∠ACD=90°﹣∠ACD,∠ACE=∠DCE+∠ACD=90°+∠ACD,即可得到∠ACE与∠BCD互补.
解:(1)∵∠BCD=45°,∠ACB=90°,
∴∠ACD=∠ACB﹣∠DCB=45°,
又∵∠DCE=90°,
∴∠ACE=∠ACD+∠DCE=45°+90°=135°;
(2)∵∠ACE=150°,∠DCE=90°,
∴∠ACD=∠ACE﹣∠DCE=150°﹣90°=60°,
又∵∠ACB=90°,
∴∠BCD=∠ACB﹣∠ACD=90°﹣60°=30°;
(3)由(1)、(2)猜想∠ACE与∠BCD互补.
理由:∵∠BCD=∠ACB﹣∠ACD=90°﹣∠ACD,
∠ACE=∠DCE+∠ACD=90°+∠ACD,
∴∠BCD+∠ACE=90°﹣∠ACD+90°+∠ACD=180°,
∴∠ACE与∠BCD互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
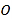 为坐标原点,矩形
为坐标原点,矩形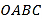 的顶点
的顶点 、
、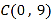 ,将矩形
,将矩形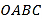 的一个角沿直线
的一个角沿直线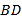 折叠,使得点
折叠,使得点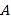 落在对角线
落在对角线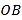 上的点
上的点 处,折痕与
处,折痕与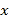 轴交于点
轴交于点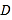 .
.(1)求线段
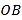 的长度;
的长度;(2)求直线
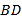 所对应的函数表达式;
所对应的函数表达式;(3)若点
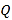 在线段
在线段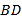 上,在线段
上,在线段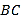 上是否存在点
上是否存在点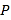 ,使以
,使以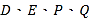 为顶点的四边形是平行四边形?若存在,请求出点
为顶点的四边形是平行四边形?若存在,请求出点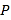 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.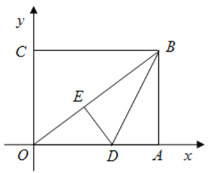
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的有( )
①用两颗钉子就可以把木条固定在墙上
②把笔尖看成一个点,当这个点运动时便得到一条线;
③把弯曲的公路改直,就能缩短路程;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上。
A.
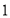 个B.
个B.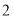 个C.
个C.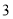 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B两点在数轴上,点A在原点O的左边,表示的数为﹣10,点B在原点的右边,且BO=3AO.点M以每秒3个单位长度的速度从点A出发向右运动.点N以每秒2个单位长度的速度从点O出发向右运动(点M,点N同时出发).
(1)数轴上点B对应的数是 ,点B到点A的距离是 ;
(2)经过几秒,原点O是线段MN的中点?
(3)经过几秒,点M,N分别到点B的距离相等?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的个数有( )
①已知直角三角形的面积为2,两直角边的比为1:2,则斜边长为
 ;
;②直角三角形的最大边长为
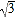 ,最短边长为1,则另一边长为
,最短边长为1,则另一边长为 ;
;③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC为直角三角形;
④等腰三角形面积为12,底边上的高为4,则腰长为5.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0), B(0,﹣1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

