【题目】在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,沿折线ABCD方向以3cm/s的速度匀速运动;点Q从点D出发,沿线段DC方向以2cm/s的速度匀速运动. 已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为t(s).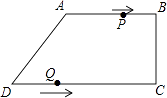
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.
参考答案:
【答案】
(1)解:如图1:过点A作AM⊥CD于点M,
∵∠BCD=90°,
即BC⊥CD,
∴AM∥BC,
又∵AB∥CD,
∴四边形ABCM为平行四边形,
∵∠BCD=90°,
∴平行四边形ABCM为矩形,
∵AB=AD=10cm,BC=8cm,
∴AM=BC=8cm,CM=AB=10cm,
在Rt△ADM中,
∴DM=![]() =6cm,
=6cm,
∴CD=CM+MD=10+6=16cm.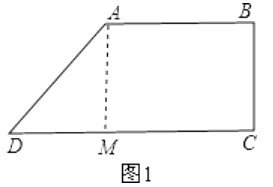
(2)解:如图2:
∵运动时间为t,
∴AP=3t,DQ=2t,
又∵AB=10cm,
∴PB=AB-AP=10-3t,
又∵四边形PBQD为平行四边形,
∴PB=DQ,
∴10-3t=2t,
∴t=2,
∴PB=DQ=4cm,
由(1)知CD=16cm,
∴CQ=12cm,
又∵BC=8cm,∠BCD=90°,
在Rt△BCQ中,
∴BQ=![]() =4
=4![]() cm,
cm,
∴CPBQD=2(PB+BQ)=2×(4+4![]() )=8+8
)=8+8![]() (cm).
(cm).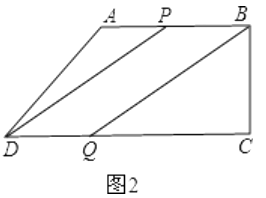
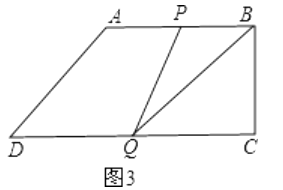
(3)解:①当P在AB上时,如图3,
∵运动时间为t,
∴AP=3t,DQ=2t,
∴0![]() 3t
3t![]() 10,
10,
∴0![]() t
t![]()
![]() ,
,
又∵AB=10cm,BC=8cm,
∴PB=AB-AP=10-3t,
∴S△BPQ=![]() .BP.BC=
.BP.BC=![]() ×(10-3t)×8=20,
×(10-3t)×8=20,
∴t=![]() .
.
②当P在BC上时,如图4,
∵运动时间为t,
∴AP=3t,DQ=2t,
∴10![]() 3t
3t![]() 18,
18,
∴![]()
![]() t
t![]() 6,
6,
又∵AB=10cm,BC=8cm,
∴PB=AB-AP=3t-10,
又由(1)知CD=16cm,
∴CQ=16-2t,
∴S△BPQ=![]() .BP.CQ=
.BP.CQ=![]() ×(3t-10)×(16-2t)=20,
×(3t-10)×(16-2t)=20,
∴3t2-34t+100=0,
∴△=342-4×3×100=-44![]() 0,
0,
∴从方程无解.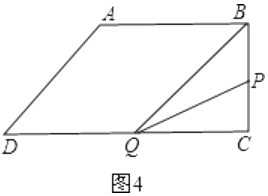
③当P在CD上时,若点P在点Q的右侧,如图5,
∵运动时间为t,
∴AP=3t,DQ=2t,
又∵AB=10cm,BC=8cm,
∴CP=AP-AB-BC=3t-18,
又由(1)知CD=16cm,
∴CQ=16-2t,
∴PQ=CQ-CP=(16-2t)-(3t-18)=34-5t,
∴![]() ,
,
∴6![]() t
t![]()
![]() .
.
∴S△BPQ=![]() .PQ.BC=
.PQ.BC=![]() ×(34-5t)×8=20,
×(34-5t)×8=20,
∴t=![]()
![]() 6(不合题意,舍去).
6(不合题意,舍去).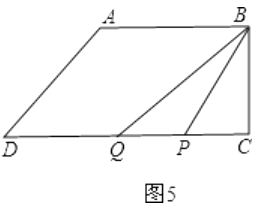
④当P在CD上时,若点P在点Q的左侧,如图6,
∵运动时间为t,
∴AP=3t,DQ=2t,
又∵AB=10cm,BC=8cm,
∴CP=AP-AB-BC=3t-18,
又由(1)知CD=16cm,
∴CQ=16-2t,
∴PQ=CP-CQ=(3t-18)-(16-2t)=5t-34,
∴![]() ,
,
∴![]()
![]() t
t![]() 8.
8.
∴S△BPQ=![]() .PQ.BC=
.PQ.BC=![]() ×(5t-34)×8=20,
×(5t-34)×8=20,
∴t=![]() .
.
综上所述:当t=![]() 秒或
秒或![]() 秒时,△BPQ的面积为20cm2.
秒时,△BPQ的面积为20cm2.
【解析】(1)如图1:过点A作AM⊥CD于点M,由∠BCD=90°,AB∥CD得出四边形ABCM为矩形,在Rt△ADM中,根据勾股定理求出DM=6cm,
从而求出CD=CM+MD=10+6=16cm.
(2)如图2:由题意得出AP=3t,DQ=2t,PB=AB-AP=10-3t,由平行四边形的性质求出t的值,从而得出PB=DQ=4cm,再由勾股定理求出
BQ的值,从而求出四边形PBQD的周长.
(3)根据题意分四种情况讨论:①当P在AB上时,如图3;②当P在BC上时,如图4;③当P在CD上时,若点P在点Q的右侧,如图5;④当P在CD上时,若点P在点Q的左侧,如图6;根据题意画出符合所有条件的图形,再由三角形的面积列出方程,求出符合范围的数值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空,将理由补充完整.
如图,
 于
于 ,
, 于
于 ,
, ,求证:
,求证: .
.
证明:∵
 ,
, (已知)
(已知)∴
 (垂直的定义)
(垂直的定义)∴
 (________________________)
(________________________)∴
 (________________________)
(________________________)∵
 (已知)
(已知)又∵
 (________________________)
(________________________)∴
 (________________________)
(________________________)∴
 (________________________)
(________________________)∴
 (________________________)
(________________________) -
科目: 来源: 题型:
查看答案和解析>>【题目】根据所学知识完成小题:
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.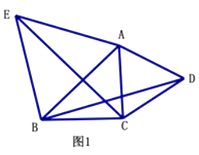
(2)【深入探究】如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.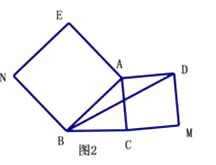
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,如图所示是小明从家到学校这一过程中所走的路程 s(米)与时间 t(分)之间的关系.
(1)小明从家到学校的路程共 米,从家出发到学校,小明共用了 分钟;
(2)小明修车用了多长时间?
(3)小明修车以前和修车后的平均速度分别是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为1的正三角形OAP沿x轴正方向连续翻转2019次,点P依次落在点P1,P2,P3,…P2019的位置,则点P2019的横坐标为( )

A. 20l9B. 2020C. 2018.5D. 2019.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知直线y=﹣
 x+4与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标为______.
x+4与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标为______. -
科目: 来源: 题型:
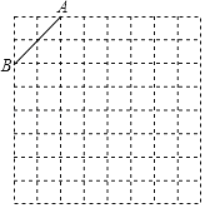
查看答案和解析>>【题目】如图是规格为8×8的正方形网格,每个小方格都是边长为1的正方形.
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4);
(2)在第二象限内的格点(网格线的交点)上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是_____.
(3)画出△ABC关于y轴对称的△A′B′C′.
相关试题

