【题目】填空,将理由补充完整.
如图,![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() ,求证:
,求证:![]() .
.

证明:∵![]() ,
,![]() (已知)
(已知)
∴![]() (垂直的定义)
(垂直的定义)
∴![]() (________________________)
(________________________)
∴![]() (________________________)
(________________________)
∵![]() (已知)
(已知)
又∵![]() (________________________)
(________________________)
∴![]() (________________________)
(________________________)
∴![]() (________________________)
(________________________)
∴![]() (________________________)
(________________________)
参考答案:
【答案】同位角相等,两直线平行;两直线平行,同位角相等;平角的定义;等量代换;等量代换;内错角相等,两直线平行
【解析】
由垂直的定义得出∠BED=∠BFC=90°;由同位角相等得出ED∥FC;由两直线平行,同位角相等,得出∠2=∠3;由∠1+∠EDC=180°,∠2+∠EDC=180°,等量代换得出∠1=∠2,等量代换得出∠1=∠3;由内错角相等,两直线平行即可得出结论.
证明:∵CF⊥AB,DE⊥AB(已知),
∴∠BED=∠BFC=90°(垂直的定义),
∴ED∥FC (同位角相等,两直线平行),
∴∠2=∠3 (两直线平行,同位角相等),
∵∠1+∠EDC=180°(已知),
又∵∠2+∠EDC=180°(平角的定义),
∴∠1=∠2 (等量代换),
∴∠1=∠3(等量代换),
∴FG∥BC (内错角相等,两直线平行).
故答案为:同位角相等,两直线平行;两直线平行,同位角相等;平角的定义;等量代换;等量代换;内错角相等,两直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】若a、b、c是正数,下列各式,从左到右的变形不能用如图验证的是( )
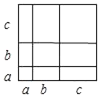
A. (b+c)2=b2+2bc+c2
B. a(b+c)=ab+ac
C. (a+b+c)2=a2+b2+c2+2ab+2bc+2ac
D. a2+2ab=a(a+2b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,四边形
 中,
中, ,
, ,
, ,且
,且 ,
,试求:(1)
 的度数;(2)四边形
的度数;(2)四边形 的面积(结果保留根号);
的面积(结果保留根号);
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据所学知识完成小题:
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.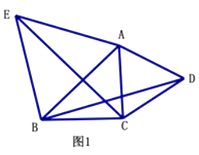
(2)【深入探究】如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.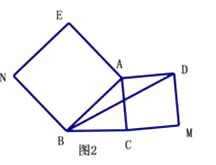
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,如图所示是小明从家到学校这一过程中所走的路程 s(米)与时间 t(分)之间的关系.
(1)小明从家到学校的路程共 米,从家出发到学校,小明共用了 分钟;
(2)小明修车用了多长时间?
(3)小明修车以前和修车后的平均速度分别是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,沿折线ABCD方向以3cm/s的速度匀速运动;点Q从点D出发,沿线段DC方向以2cm/s的速度匀速运动. 已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为t(s).
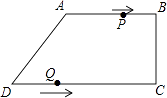
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.
相关试题

