【题目】根据所学知识完成小题:
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.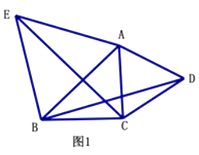
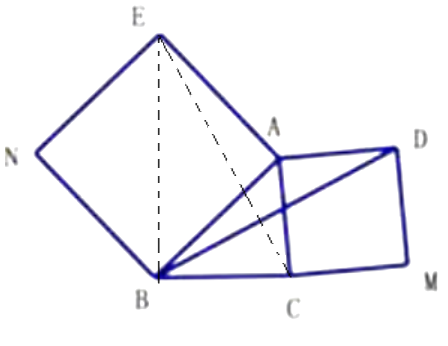
(2)【深入探究】如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.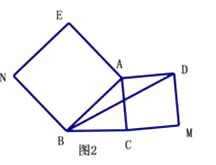
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.
参考答案:
【答案】
(1)解:BD=CE,理由如下:
∵△ABE和△ACD均是等边三角形,
∴AB=AE,AD=AC,∠BAE=∠CAD=60°,
∴∠BAE+∠BAC=∠CAD+∠BAC,
即∠CAE=∠BAD,
在△CAE和△BAD中,
∵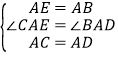 ,
,
∴△CAE≌△BAD,
∴CE=BD,
(2)解:连接BE,CE,如图:
∵四边形ABNE和四边形ACMD均是正方形,
∴AE=AB,AC=AD,∠BAE=∠CAD=90°,
∴∠BAE+∠BAC=∠CAD+∠BAC,
即∠CAE=∠BAD,
在△CAE和△BAD中,
∵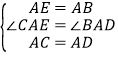 ,
,
∴△CAE≌△BAD,
∴CE=BD,
又∵四边形ABNE正方形,AB=5cm
∴∠ABE=45°,BE=5![]() ,
,
∵∠ABC=45°,
∴∠CBE=∠ABE+∠ABC=90°,
又∵BC=3cm,
∴CE=![]() =
=![]() ,
,
∴BD=![]() .
.
(3)解:作AE⊥AB,交BC延长线于点E,如图:
∴∠BAE=90°,
∵∠ABC=45°,
∴AB=AE,
又∵△ACD为等腰直角三角形
∴AD=AC,∠DAC=90°,
∴∠CAE+∠BAC=∠DAB+∠BAC,
即∠CAE=∠BAD,
在△CAE和△BAD中,
∵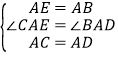 ,
,
∴△CAE≌△BAD,
∴CE=BD,
在Rt△CAB中,
∵AB=AE=5cm,BC=3cm,
∴BE=5![]() cm,
cm,
∴CE=BE-BC=5![]() -3(cm),
-3(cm),
∴BD=5![]() -3(cm).
-3(cm).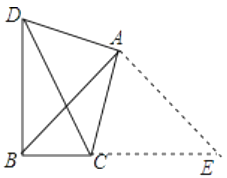
【解析】(1)BD=CE,理由如下:
由等边三角形的性质得出AB=AE,AD=AC,∠BAE=∠CAD=60°,再由等量代换得出∠CAE=∠BAD,根据SAS得出△CAE≌△BAD,再由全等三角形的对应边相等得出CE=BD.
(2)连接BE,CE,如图:由正方形的性质得出AE=AB,AC=AD,∠BAE=∠CAD=90°,再由等量代换得出∠CAE=∠BAD,根据SAS得出△CAE≌△BAD,再由全等三角形的对应边相等得出CE=BD;再由正方形性质得出,BE=5![]() ,结合已知条件得出∠CBE=90°,根据勾股定理得出CE=
,结合已知条件得出∠CBE=90°,根据勾股定理得出CE=![]() ,即BD的长.
,即BD的长.
(3)作AE⊥AB,交BC延长线于点E,如图:由垂直和等腰三角形的性质得出AB=AE,AD=AC,再由等量代换得出∠CAE=∠BAD,根据SAS得出△CAE≌△BAD,再由全等三角形的对应边相等得出CE=BD;在Rt△CAB中,由勾股定理得出BE值,从而求出BD长.
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°),还要掌握等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM=
 AD,点N是折线AB﹣BC上的一个动点.
AD,点N是折线AB﹣BC上的一个动点.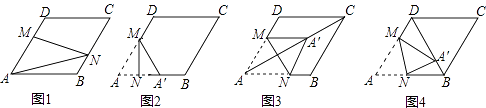
(1)如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .
(2)当点N在AB边上时,将△AMN沿MN翻折得到△A′MN,如图2,
①若点A′落在AB边上,则线段AN的长度为;
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
③当点A′落在对角线BD上时,如图4,求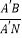 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:2x+7+3x﹣2,其中x=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中的真命题是
A. 同位角相等B. 在同一平面内,如果a⊥b,b⊥c,则a⊥c
C. 相等的角是对顶角D. 在同一平面内,如果a∥b,b∥c,则a∥c
-
科目: 来源: 题型:
查看答案和解析>>【题目】为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列不等式:a的相反数的绝对值与3的和是正数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】向阳村2010年的人均收入为12000元,2012年的人均收入为14520元,求人均收入的年平均增长率.
相关试题

