搜索
【题目】如图，将边长为1的正三角形OAP沿x轴正方向连续翻转2019次，点P依次落在点P1，P2，P3，…P2019的位置，则点P2019的横坐标为( )
A. 20l9B. 2020C. 2018.5D. 2019.5
参考答案：
【答案】C
【解析】
分析题意，根据等边三角形的性质和翻折的性质，可得到P1、P2的横坐标是1，P3的横坐标是2.5，P4、P5的横坐标是4，P6的横坐标是5.5，观察各点横坐标的变化可得P3n-2的横坐标为3n-2，P3n-1的横坐标为3n-2，P3n的横坐标为3n-0.5；接下来根据2019=3×673，利用上述规律即可得出点P2019的横坐标.
观察图形结合翻转的方法可以得出P1、P2的横坐标是1，P3的横坐标是2.5；
P4、P5的横坐标是4，P6的横坐标是5.5；
P7、P8的横坐标是7，P9的横坐标是8.5；
…
依此类推下去，P3n-2的横坐标为3n-2，P3n-1的横坐标为3n-2，P3n的横坐标为3n-0.5，
2019=3×673，
所以P2019的横坐标为3×673-0.5=2018.5．
故选：C.
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据所学知识完成小题：
（1）如图1，锐角△ABC中，分别以AB、AC为边向外作等边△ABE和等边△ACD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．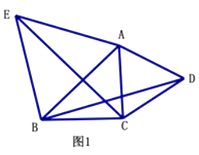
（2）【深入探究】如图2，△ABC中，∠ABC=45°，AB=5cm，BC=3cm，分别以AB、AC为边向外作正方形ABNE和正方形ACMD，连接BD，求BD的长．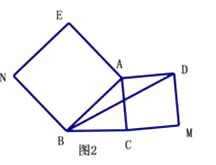
（3）如图3，在（2）的条件下，以AC为直角边在线段AC的左侧作等腰直角△ACD，求BD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某天小明骑自行车上学，途中因自行车发生故障，修车耽误了一段时间后继续骑行，按时赶到了学校，如图所示是小明从家到学校这一过程中所走的路程 s（米）与时间 t（分）之间的关系．
（1）小明从家到学校的路程共 米，从家出发到学校，小明共用了 分钟；
（2）小明修车用了多长时间？
（3）小明修车以前和修车后的平均速度分别是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在四边形ABCD中，AB∥CD，∠BCD=90°，AB=AD=10cm，BC=8cm，点P从点A出发，沿折线ABCD方向以3cm/s的速度匀速运动；点Q从点D出发，沿线段DC方向以2cm/s的速度匀速运动. 已知两点同时出发，当一个点到达终点时，另一点也停止运动，设运动时间为t（s）.
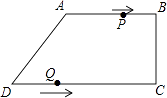
（1）求CD的长；
（2）当四边形PBQD为平行四边形时，求四边形PBQD的周长；
（3）在点P、Q的运动过程中，是否存在某一时刻，使得△BPQ的面积为20cm2？若存在，请求出所有满足条件的t的值；若不存在，请说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，已知直线y＝﹣
x+4与x轴、y轴分别交于A、B两点，点C(0，n)是y轴上一点．把坐标平面沿直线AC折叠，使点B刚好落在x轴上，则点C的坐标为______． -
科目： 来源： 题型：
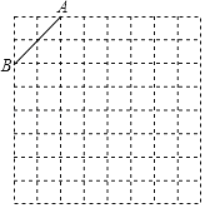
查看答案和解析>>【题目】如图是规格为8×8的正方形网格，每个小方格都是边长为1的正方形．
(1)在网格中建立平面直角坐标系，使A点坐标为(﹣2，4)；
(2)在第二象限内的格点(网格线的交点)上画一点C，使点C与线段AB组成一个以AB为底的等腰三角形，且腰长是无理数，则C点坐标是_____．
(3)画出△ABC关于y轴对称的△A′B′C′．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥DF，交AB于点E，连结EG、EF．
（1）求证：BG＝CF．
（2）请你判断BE+CF与EF的大小关系，并说明理由．
相关试题
