【题目】七年级教材在图形与几何部分给出了五条基本事实,在《证明》一章中我们从两条基本事实出发,把前面得到的平行线相关性质进行了严格的证明,体会了数学的公里化思想.请完成下列证明活动:
(1)活动 ![]() .利用基本事实证明:“两直线平行,同位角相等”.(在括号内填上相应的基本事实)
.利用基本事实证明:“两直线平行,同位角相等”.(在括号内填上相应的基本事实)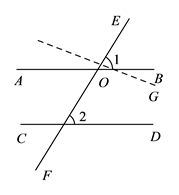
已知:如图,直线 ![]() 、
、 ![]() 被直线
被直线 ![]() 所截,
所截, ![]() .
.
求证: ![]() .
.
证明:假设 ![]() ,则可以过点
,则可以过点 ![]() 作
作 ![]() .
.
∵ ![]() ,
,
∴ ![]() ().
().
∴过 ![]() 点存在两条直线
点存在两条直线 ![]() 、
、 ![]() 两条直线与
两条直线与 ![]() 平行,这与基本事实()矛盾.
平行,这与基本事实()矛盾.
∴假设不成立.
∴ ![]() .
.
(2)活动 ![]() .利用刚刚证明的“两直线平行,同位角相等”证明“两直线平行,同旁内角互补”.(要求画图,写出已知、求证并写出证明过程)
.利用刚刚证明的“两直线平行,同位角相等”证明“两直线平行,同旁内角互补”.(要求画图,写出已知、求证并写出证明过程)
已知:.
求证:.
证明: .
参考答案:
【答案】
(1)同位角相等两直线平行;AB∥CD
(2)AB∥CD;两直线平行,同旁内角互补;如图,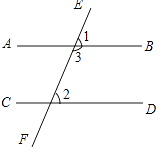
∵AB∥CD,
∴∠1=∠2.
∵∠1+∠3=180°,
∴∠2+∠3=180°,即两直线平行,同旁内角互补.
【解析】(1)证明:假设 ![]() ,则可以过点
,则可以过点 ![]() 作
作 ![]() .
.
∵ ![]() ,
,
∴ ![]() (同位角相等,两直线平行).
(同位角相等,两直线平行).
∴过 ![]() 点存在两条直线
点存在两条直线 ![]() 、
、 ![]() 两条直线与
两条直线与 ![]() 平行,这与基本事实(AB∥CD)矛盾.
平行,这与基本事实(AB∥CD)矛盾.
∴假设不成立.
∴ ![]() .
.
所以答案是:同位角相等,两直线平行;AB∥CD
( 2 )已知:AB∥CD,
求证:两直线平行,同旁内角互补.
证明:如图,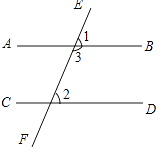
∵AB∥CD,
∴∠1=∠2.
∵∠1+∠3=180°,
∴∠2+∠3=180°,即两直线平行,同旁内角互补.
【考点精析】掌握平行线的判定与性质和反证法是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;先假设命题中的结论不成立,然后由此经过推理,引出矛盾,判定所做的假设不正确,从而得到原命题成立,这种证明方法叫做反证法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数的图象y1=kx+b与反比例函数
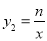 的图象交于点A(1,5)和点B(m,1).
的图象交于点A(1,5)和点B(m,1).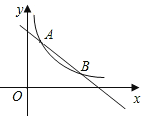
(1)求m的值和反比例函数的解析式;
(2)当x>0时,根据图象直接写出不等式
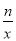 ≥kx+b的解集;
≥kx+b的解集;(3)若经过点B的抛物线的顶点为A,求该抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  与
与  的角平分线交于
的角平分线交于 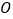 点.
点.
(1)若 ,则
,则 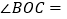
 ;
;
(2)若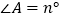 ,则
,则 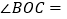
 ;
;
(3)若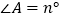 ,
,  与
与  的角平分线交于
的角平分线交于 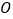 点,
点,  的平分线与
的平分线与  的平分线交于点
的平分线交于点 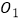 ,
,  ,
,  的平分线与
的平分线与 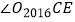 的平分线交于点
的平分线交于点 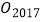 ,则
,则 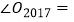
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,AB=2AD.
(1)作AE平分∠BAD交DC于E(尺规作图,保留作图痕迹);
(2)在(1)的条件下,连接BE,判定△ABE的形状(不要求证明).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:3a=2,3b=6,3c=18,试确定a、b、c之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣x2+bx+c经过点(﹣1,2).
(1)用含b的代数式表示c;
(2)该抛物线与x轴有几个交点?为什么?
-
科目: 来源: 题型:
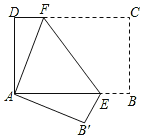
查看答案和解析>>【题目】如图,将长方形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.
(1)证明:△ADF≌△AB′E;
(2)若AD=12,DC=18,求△AEF的面积.
相关试题

