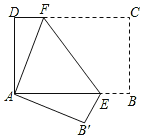
【题目】如图,将长方形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.
(1)证明:△ADF≌△AB′E;
(2)若AD=12,DC=18,求△AEF的面积.
参考答案:
【答案】(1)证明见解析(2)78
【解析】试题分析:(1)利用两角夹边对应相等的两个三角形全等即可判定.
(2)利用三角形面积公式求解即可.
试题解析:(1)∵四边形ABCD是矩形,
∴∠D=∠C=∠B′=90°,AD=CB=AB′,
∵∠DAF+∠EAF=90°,∠B′AE+∠EAF=90°,
∴∠DAF=∠B′AE,
在△ADF和△AB′E中
 ,
,
∴△ADF≌△AB′E.
(2)解:由折叠性质得FA=FC,设FA=FC=x,则DF=DC-FC=18-x,
在Rt△ADF中,AD2+DF2=AF2,
∴![]() .
.
解得![]() .
.
∵△ADF≌△AB′E,
∴AE=AF=13.
∴S△AEF= ![]() =
=![]() =78.
=78.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级教材在图形与几何部分给出了五条基本事实,在《证明》一章中我们从两条基本事实出发,把前面得到的平行线相关性质进行了严格的证明,体会了数学的公里化思想.请完成下列证明活动:
(1)活动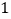 .利用基本事实证明:“两直线平行,同位角相等”.(在括号内填上相应的基本事实)
.利用基本事实证明:“两直线平行,同位角相等”.(在括号内填上相应的基本事实)
已知:如图,直线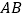 、
、 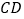 被直线
被直线 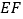 所截,
所截, 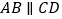 .
.
求证: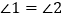 .
.
证明:假设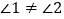 ,则可以过点
,则可以过点 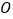 作
作 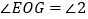 .
.
∵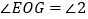 ,
,
∴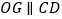 ().
().
∴过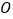 点存在两条直线
点存在两条直线 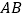 、
、 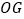 两条直线与
两条直线与 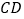 平行,这与基本事实()矛盾.
平行,这与基本事实()矛盾.
∴假设不成立.
∴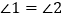 .
.
(2)活动 .利用刚刚证明的“两直线平行,同位角相等”证明“两直线平行,同旁内角互补”.(要求画图,写出已知、求证并写出证明过程)
.利用刚刚证明的“两直线平行,同位角相等”证明“两直线平行,同旁内角互补”.(要求画图,写出已知、求证并写出证明过程)
已知:.
求证:.
证明: . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:3a=2,3b=6,3c=18,试确定a、b、c之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣x2+bx+c经过点(﹣1,2).
(1)用含b的代数式表示c;
(2)该抛物线与x轴有几个交点?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)如图①,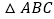 的内角
的内角  的平分线与外角
的平分线与外角 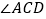 的平分线相交于
的平分线相交于 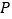 点,
点, 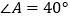 ,求
,求 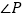 的度数.
的度数.
(2)如图,四边形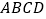 中,设
中,设 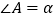 ,
, 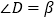 ,
, 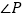 为四边形
为四边形 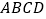 的内角
的内角  与外角
与外角 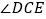 的平分线所在直线相交而形成的锐角.
的平分线所在直线相交而形成的锐角.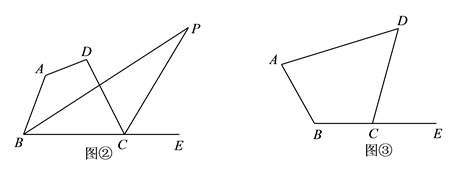
①如图②,若 ,求
,求 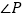 的度数.(用
的度数.(用 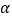 、
、 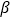 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】中秋佳节我国有赏月和吃月饼的传统,英才学校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)请根据统计图完成下列问题:
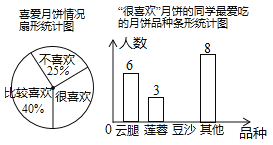
(1)扇形统计图中,“很喜欢”的部分所对应的圆心角为 度;条形统计图中,“很喜欢”月饼中喜欢“豆沙”月饼的学生有 人;
(2)若该校共有学生1200人,请根据上述调查结果,估计该校学生中“很喜欢”月饼的有 人.
(3)李民同学最爱吃莲蓉月饼,陈丽同学最爱吃豆沙月饼,现有重量、包装完全一样的豆沙、莲蓉、蛋黄
三种月饼各一个,让李民、陈丽每人各选一个,则李民、陈丽两人都选中自己最爱吃的月饼的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸中,△ABC的三个顶点及D、E、F、G、H、五个点分别位于小正方形的顶点上.
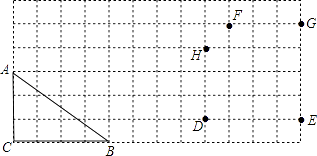
(1)画出△ABC绕点B顺时针方向旋转90°后的图形.
(2)先从E、F、G、H四个点中任意取两个不同的点,再和D点构成三角形,求所得三角形与△ABC面积相等的概率是 .
相关试题

