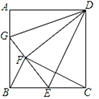
【题目】如图,已知正方形ABCD的边长为12,E是BC中点,将正方形边CD沿DE折叠到DF,将AD折叠,使AD与DF重合,折痕交AB于G,连接BF,CF,则下列结论:①G、F、E三点共线;②BG=8;③△BEF∽△CDF;④S△BFG=![]() .其中正确的有( )
.其中正确的有( )
A. ①② B. ①②③ C. ②③④ D. ①②③④
参考答案:
【答案】D
【解析】分析:根据已知条件易证∠GFD+∠DFE=180°,即可得点G、F、E共线,①正确;设BG=x,则GF=AG=12-x,Rt△BEG中根据勾股定理求得x的值,即可判定②正确;根据折叠的性质和已知条件证得∠CDF=∠BEF,再由BE=FE,FD=CD,即可判定△BEF∽△CDF,③正确;在Rt△BEG中,根据面积法可得EG边上的高为![]() ,根据三角形的面积公式即可求得S△BFG=
,根据三角形的面积公式即可求得S△BFG=![]() ,④正确.
,④正确.
详解:由题意得∠GFD=∠DFE=90°,
∴∠GFD+∠DFE=180°,故点G、F、E共线,故①正确;
设BG=x,则GF=AG=12-x,
由题意得:EF=CE=BE=6,
在Rt△BEG中,有BG2+BE2=EG2,
![]()
解得x=8,故②正确;
在四边形DCEF中,
∵∠DFE=∠DCE=90°,
∴∠CEF+∠CDF=180°,
又∠CEF+∠BEF=180°,
∴∠CDF=∠BEF,
∵BE=FE,FD=CD,
∴△BEF∽△CDF,故③正确;
在Rt△BEG中,根据面积法可得EG边上的高为![]() ,又FG=4,∴S△BFG=
,又FG=4,∴S△BFG=![]() ,故④正确;
,故④正确;
所以正确的有①②③④,故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】透明的口袋里装有3个球,这3个球分别标有数字1、2、3,这些球除了数字外都相同。
(1)如果从袋中任意摸出一个球,那么摸到标有数字是2的球的概率是多少?(3分)
(2)小明和小东玩摸球游戏,游戏规则如下:先由小明随机摸出一个球,记下球的数字后放回,搅匀后再由小东随机摸出一个球,记下球的数字.谁摸出的球的数字大,谁获胜.现请你利用树状图或列表的方法分析游戏规则对双方是否公平?并说明理由。(6分)
-
科目: 来源: 题型:
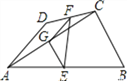
查看答案和解析>>【题目】如图,四边形 ABCD 中,AD=BC,E、F、G 分别是 AB、CD、AC 的中点,若∠DAC=20 ,∠ACB=90 ,则 ∠FEG=( )
A.
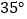 B.
B. 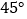 C.
C. 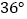 D.
D. 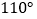
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,∠B=60°.G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF,下列说法不正确的是( )
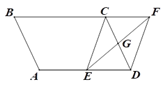
A. 四边形CEDF是平行四边形
B. 当
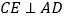 时,四边形CEDF是矩形
时,四边形CEDF是矩形C. 当
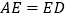 时,四边形CEDF是菱形
时,四边形CEDF是菱形D. 当
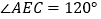 时,四边形CEDF是菱形
时,四边形CEDF是菱形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
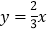 与双曲线
与双曲线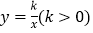 交于A、B两点,A点的横坐标为3,则下列结论:①k=3;②关于x的不等式
交于A、B两点,A点的横坐标为3,则下列结论:①k=3;②关于x的不等式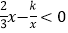 的解集为
的解集为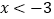 或
或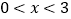 ;③若双曲线
;③若双曲线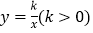 上有一点C的纵坐标为6,则△AOC的面积为8;④若在
上有一点C的纵坐标为6,则△AOC的面积为8;④若在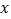 轴上有一点M,
轴上有一点M,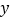 轴上有一点N,且点M、N、A、C四点恰好构成平行四边形,则M、N点的坐标分别为M(2,0)、N(0,4),其中正确结论的个数( )
轴上有一点N,且点M、N、A、C四点恰好构成平行四边形,则M、N点的坐标分别为M(2,0)、N(0,4),其中正确结论的个数( )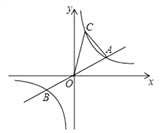
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
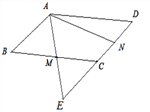
查看答案和解析>>【题目】如图,在平行四边形ABCD中,M,N分别为BC,CD的中点,AM=1,AN=2,∠MAN=60°,AM ,DC的延长线相交于点E,则AB的长为_____________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行了调查,随机调查了
 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
(1)根据图中信息求出
 =___________,
=___________, =_____________;
=_____________;(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生种,大约有多少人最认可“微信”这一新生事物?
相关试题

